Двойственность в линейном программировании. Одновременное решение пары двойственных задач линейного программирования

Вычислительная математика

   Специальность ПО         

4-й семестр

Конспект лекций

Лекция 11

            Двойственность в линейном программировании. Одновременное решение пары двой-ственных задач линейного программирования.

1.  Определение пары двойственных задач линейного программирования.

            Напомним, что основная задача линенйного программирования - это задача поиска максимума линейной функции

при ограничениях

.

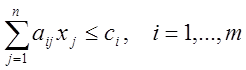Предположим теперь, что среди только что указанных ограничений присутствуют точные равенства и для определенности будем считать, что для  имеют место неточные равенства, а для  - равенства точные:

.

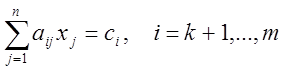Ясно, что такое предположение не уменьшает общности задачи. Предположим, далее (и это тоже не уменьшит общность задачи), что имеются несвободные неизвестные  и свободные .

            Задачей, двойственной к ОЗЛП, называется задача поиска минимума линейной функции

при ограничениях:

,

,

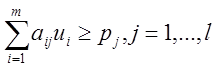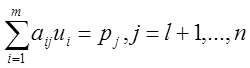а также при несвободных неизвестных , и свободных неизвестных . Здесь надо обратить внимание, что целевая функция двойственной задачи получается из коэффициентов, которые равны правым частям в исходных ограничениях, огра-ичения в двойственной задаче соответствуют столбцам матрицы коэффициентов исходной ОЗЛП, причем ограничения-неравенства соответствуют несвободным неизвестным, а огра-ичения-равенства соттветствуют свободным переменным; наконец, несвободные переменные в двойственной задаче соответствуют неравенствам исходной ОЗЛП, а свободные переменные двойственной задачи соответствуют равенствам исходной ОЗЛП.

            Обе сформулированные задачи называются парой двойственных задач. О таких парах доказывается следующее принципиальное положение:

1) существует тогда и только тогда, когда существует и при этом имеет

место равенство: ;

2) если одна из задач противоречива, то другая либо тоже противоречива, либо неогра-

ниченна;

3) если одна из задач неограниченна, то другая противоречива.

        2. Одновременное решение пары двойственных задач линейного программирования.

Нетрудно заметить, что двойственная задача к основной задаче линейного программиро- вания сама является задачей линейного программирования. Как показывалось выше, ее можно привести к каноническому виду основной задачи линейного программирования и, следователь-но, решить симплекс-методом. Последний представляет собой определенные действия с кон-кретной числовой таблицей.

            Если сравнить числовую таблицу, используемую при симплекс-методе для основной задачи линенйного программирования, с числовой таблицей, используемой при симплекс-методе для двойственной задачи, то окажется, что решения этих двух задач можно провести одновременно, манипулируя с одной и той же таблицей. Воспроизведем эту таблицу:

		v1=	...	vj=	...	vn=	w=
		-x1	...	-xj	...	-xn	1
u1	y1=	a11	...	a1j	...	a1n	c1
...	...	...	...	...	...	...	...
ui	yi=	ai1	...	ai,j	...	ai,n	ci
...	...	...	...	...	...	...	...
um	ym=	am1	...	am,j	...	am,n	cm
1	z=	-p1	...	-pj	...	-pn	0

Можно заметить, что проведение симплекс-метода с этой таблицей в отношении переменных x_j, y_i  дает решение и для двойственной задачи, если на каждом шагу менять местами и соот-ветствующие u_i, v_j. Мы продемонстрируем это ниже на конкретном примере.

3.  Пример одновременного решения пары двойственных задач линейного програм-

мирования.

Итак, требуется решить одновременно две экстремальные задачи. Задача первая:

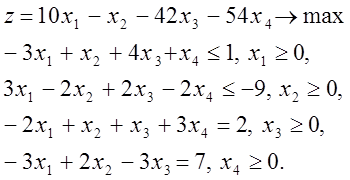
            Прежде, чем записать вторую задачу, сформируем стандартную рабочую таблицу для пары двойственных задач, следуя правилу из предыдущего пункта:

		v1=	v2=	v3=	v4=	w=
		-x1	-x2	-x3	-x4	1
u1	y1=	-3	1	4	1	1
u2	y2=	3	-2	2	-2	-9
u3	0	-2	1	1	3	2
u4	0	-3	2	-3	0	7
1	z=	-10	1	42	54

            Теперь по таблице нам легче будет записать условие двойственной задачи.

А именно:

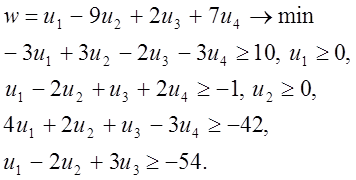
Таким образом, переменные u₃, u₄ - свободные. Алгоритм симплекс-метода нам уже известен из предыдущего изложения; поэтому будем лишь указывать разрешающие элементы для оче-редных модифицированных жордановых исключений (как обычно, разрешающий элемент вы-деляется в табюлице серым фоном):