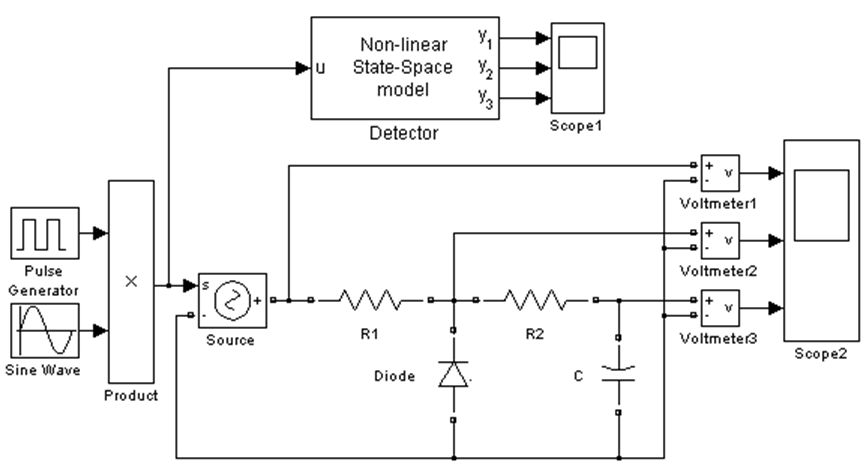
Рис. 11 Модель детектора в Simulink
Частота заполнения импульсов 1кГц,
длительность импульса равна 50 периодов синусоиды, скважность 25%. В настройках
блока Sine Wave задаём параметр Frequency
равным 2*pi*1000, а в настройках блока Pulse Generator
параметр Period 4*50/1000 и параметр Pulse Width
25. Сопротивления ![]() , ёмкость конденсатора
, ёмкость конденсатора ![]() . Для работы примера необходимо определить
в Matlab переменные:
. Для работы примера необходимо определить
в Matlab переменные:
R1 = 5e3;
R2 = 5e3;
C = 1e-6;
Эти переменные необходимо указать в настройках соответствующих элементах модели. В настройках диода все параметры задать равными нулю кроме Resistance Ron, которое оставить равным 0,001. В настройках решателя Simulation–>Configuration parameters... на странице Solver из списка Type выбрать Fixed-step, а в поле Fixed-step size задать 5e-5, в поле Stop time задать 0,1. Для значительного сокращения времени вычислений рекомендуется использовать решатель с постоянным шагом по времени, если используются нелинейные элементы. В качестве решатели можно использовать ode3, который устанавливается по умолчанию, когда выбирается решатель с постоянным шагом. В модели (рис. 11) измеряются напряжения в трёх точках: Voltmeter1 – напряжение на источнике (входной сигнал), Voltmeter2 – напряжение на диоде, Voltmeter3 – напряжение на конденсаторе (выходной сигнал).
Для того чтобы
написать уравнение состояния, рассмотрим работу схемы (рис. 11). В зависимости
от напряжения на диоде возможны два случая. Один когда на диоде запирающая
разность потенциалов, тогда схема на рис. 11 может быть описана как
интегрирующая цепочка (рис. 12а). Другой когда диод открыт, тогда конденсатор
разряжается через сопротивление ![]() (рис. 12б).
(рис. 12б).
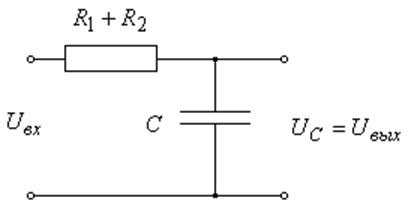
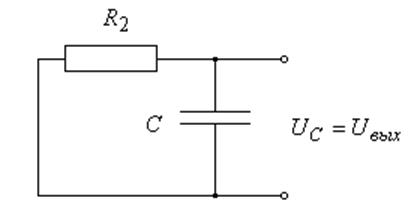
а) диод закрыт б) диод открыт
Рис. 12 Упрощённые схемы детектора
Сначала найдём условие, при котором диод закрыт.
![]() (31)
(31)
где ![]() –
напряжение на диоде,
–
напряжение на диоде, ![]() – падение напряжения на первом
сопротивлении. Чтобы найти
– падение напряжения на первом
сопротивлении. Чтобы найти ![]() , используем закон Ома,
считая диод закрытым.
, используем закон Ома,
считая диод закрытым.
 (32)
(32)
где ![]() – ток
через сопротивления,
– ток
через сопротивления, ![]() – напряжение на конденсаторе.
Подставив (32) в (31) получим неравенство:
– напряжение на конденсаторе.
Подставив (32) в (31) получим неравенство:
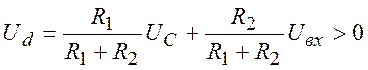 (33)
(33)
Теперь напишем уравнение состояния для случая с закрытым диодом, а потом сделаем переход к уравнению для случая с открытым диодом. Уравнение для конденсатора, уравнения Кирхгофа и закон Ома для схемы, показанной на рис. 12а:
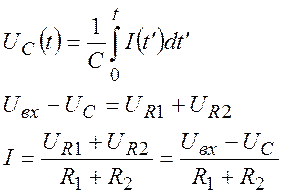 (34)
(34)
Введём те же обозначения, что и в
предыдущих примерах ![]() ,
, ![]() . В
схеме на рис. 11 на осциллограф выводятся напряжения в трёх контрольных точках,
значит ещё необходимо добавить в систему три выходных параметра. Первый
параметр – входное напряжение
. В
схеме на рис. 11 на осциллограф выводятся напряжения в трёх контрольных точках,
значит ещё необходимо добавить в систему три выходных параметра. Первый
параметр – входное напряжение ![]() , второй параметр
, второй параметр ![]() – напряжение на диоде (33), третий
параметр – выходное напряжение или напряжение на конденсаторе
– напряжение на диоде (33), третий
параметр – выходное напряжение или напряжение на конденсаторе ![]() . Тогда уравнение состояния и выходные
параметры в новых обозначениях при закрытом диоде:
. Тогда уравнение состояния и выходные
параметры в новых обозначениях при закрытом диоде:
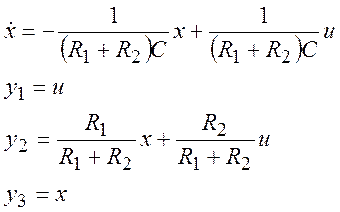 (35)
(35)
Условие (33) в новых обозначениях:
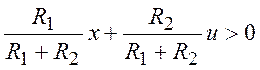 (36)
(36)
Теперь сделаем переход от схемы,
показанной на рис. 12а, к схеме на рис. 12б. Для этого надо сделать ![]() и соединить проводником вход и общий
провод, что равносильно
и соединить проводником вход и общий
провод, что равносильно ![]() . Если приравнять к нулю
эти величины в (35), получим уравнения для случая с открытым диодом:
. Если приравнять к нулю
эти величины в (35), получим уравнения для случая с открытым диодом:
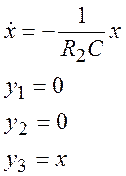 (37)
(37)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.