![]() (9)
(9)
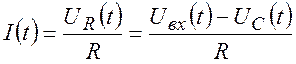 (10)
(10)
Чтобы получить уравнение состояния надо продифференцировать (8) по времени и подставить в него выражение для тока (10). Уравнением для выходных параметров системы является выражение (9). Формулы (5) и (7) для дифференцирующей цепочки:
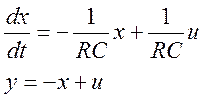 (11)
(11)
Используем уравнения (11), чтобы смоделировать прохождение прямоугольных импульсов через дифференцирующую цепочку. В Simulink есть специальный блок Simulink\Continuous\State-Space, позволяющий задать линейную систему с распределёнными параметрами с помощью матриц A, B, C, D из (5) и (7). Для сравнения результата, решаем эту же задачу с помощью SimPowerSystem (рис. 3).
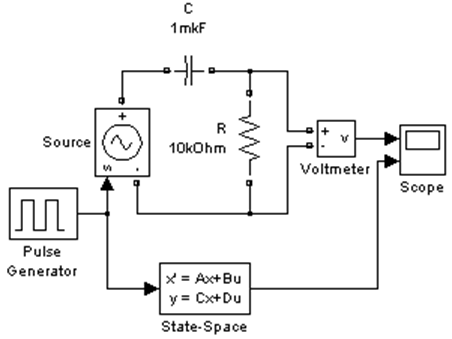
Рис. 3 Модель дифференцирующей цепочки в Simulink
В окне
параметров блока State-Space
(рис. 4) необходимо задать четыре матрицы и вектор состояния ![]() в начальный момент времени. В данном
примере порядок системы
в начальный момент времени. В данном
примере порядок системы ![]() и один входной и
выходной параметр, поэтому вместо матриц задаём соответствующие коэффициенты из
(11).
и один входной и
выходной параметр, поэтому вместо матриц задаём соответствующие коэффициенты из
(11).
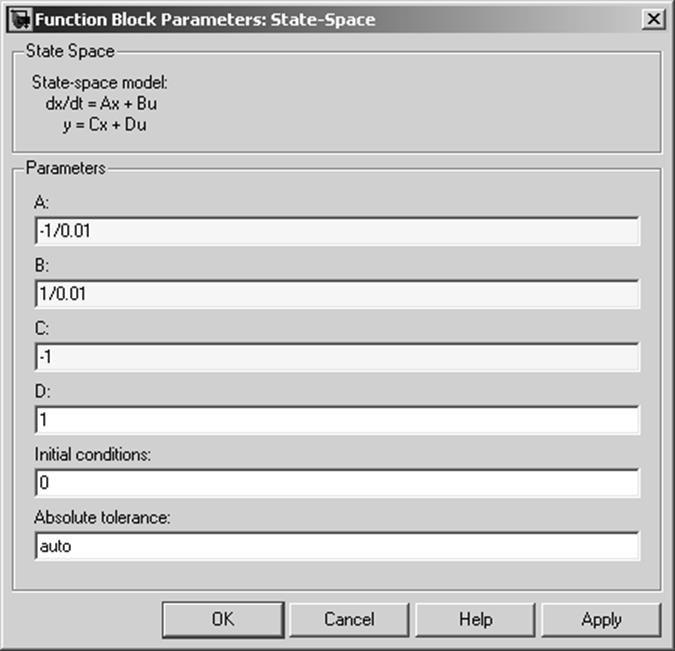
Рис. 4 Параметры блока State-Space
Пример 2
Написать уравнения состояния для линейной системы второго порядка (рис. 5) и выполнить переход от уравнений состояния к дифференциальному уравнению второго порядка.
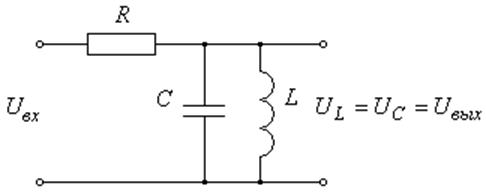
Рис. 5 Линейная система второго порядка
Также как и в предыдущем примере
выберем величины, которые могут быть выражены через интегралы по времени.
Такими величинами являются напряжение на конденсаторе ![]() и
ток через индуктивность
и
ток через индуктивность ![]() , считаем, что при
, считаем, что при ![]() эти величины были равны нулю (нулевые
начальные условия):
эти величины были равны нулю (нулевые
начальные условия):
 (12)
(12)
где ![]() – ток
через конденсатор,
– ток
через конденсатор, ![]() – напряжение на индуктивности.
Компоненты вектора состояния соответственно будут
– напряжение на индуктивности.
Компоненты вектора состояния соответственно будут ![]() и
и ![]() , входной параметр модели – напряжение,
подаваемое на вход цепочки
, входной параметр модели – напряжение,
подаваемое на вход цепочки ![]() , выходной параметр –
, выходной параметр – ![]() . Продифференцируем (12) и подставим в них
новые обозначения:
. Продифференцируем (12) и подставим в них
новые обозначения:
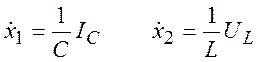 (13)
(13)
Теперь необходимо выразить ![]() и
и ![]() через
через ![]() ,
, ![]() и
и ![]() . Для этого используем следующие равенства:
. Для этого используем следующие равенства:
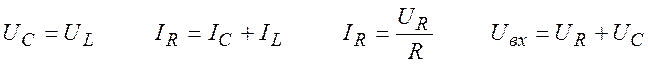 (14)
(14)
где ![]() – ток
через сопротивление,
– ток
через сопротивление, ![]() – падение напряжение на
сопротивлении. Из (14) находим выражение для тока в конденсаторе:
– падение напряжение на
сопротивлении. Из (14) находим выражение для тока в конденсаторе:
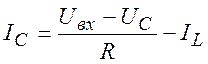 (15)
(15)
Подставляя (14) и (15) в (13) и применив новые обозначения, получаем уравнения состояния и уравнение для выходного параметра.
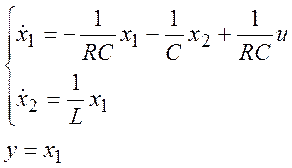 (16)
(16)
Те же уравнения, только в матричной форме, так как для блока State-Space в Simulink потребуется задать матрицы:
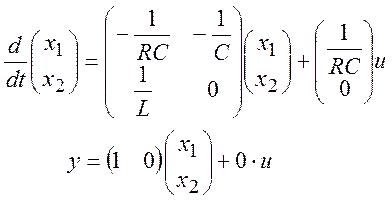 (17)
(17)
Построим эту модель в Simulink и сравним результат, выдаваемый блоком State-Space с результатом, полученным с помощью SymPowerSystem (рис. 6).
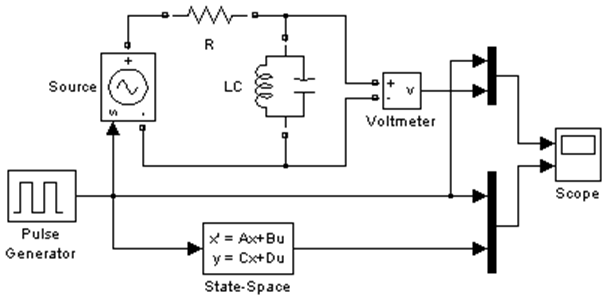
Рис .6 Модель системы второго порядка в Simulink
В диалоговом окне блока State-Space задаём следующие параметры (рис. 7):
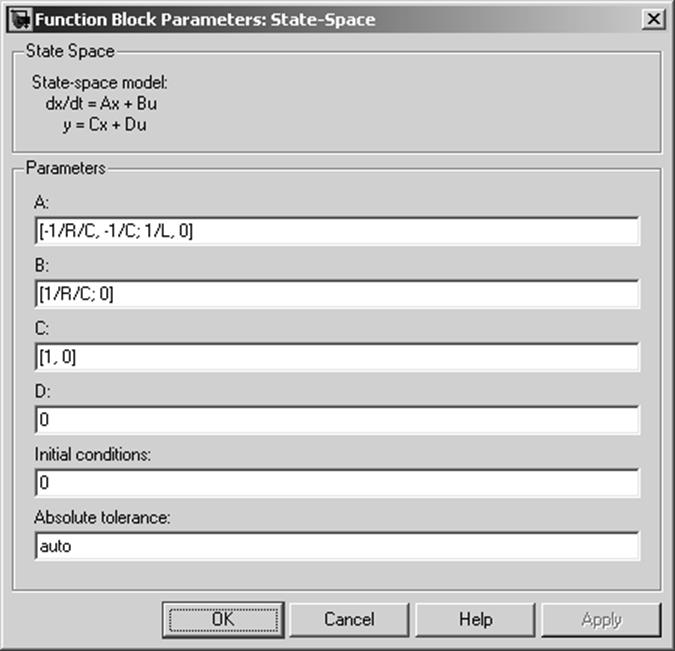
Рис. 7 Диалоговое окно блока State-Space
В командной строке Matlab определяем необходимые переменные:
R = 1e4;
C = 1e-6;
L = 2.5;
В диалоговом окне блока Puls Generator задаём период повторения импульсов 0,02 секунды и оставляем скважность 50%. В диалоговых окнах для элементов цепи указываем имена соответствующих переменных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.