Пространство состояний (State-Space). Линейные системы с сосредоточенными параметрами (line and time-invariant system – LTI), страница 3

Для того чтобы выполнить переход от системы уравнений состояния к дифференциальному уравнению второго порядка, применим преобразование Лапласа к уравнениям системы. Операция дифференцирования заменится на умножение на , а при обратном преобразовании соответственно происходит обратная замена. Применив преобразование Лапласа к (16), получим систему линейных алгебраических уравнений 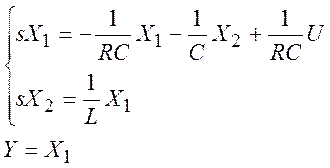(18):

                                                                                                                              (18)

где , , ,  – Лаплас-образы функций , , ,  соответственно. Умножим первое уравнение на , затем в первом уравнении заменим , воспользовавшись вторым уравнением, и, воспользовавшись третьем уравнением, в первом заменим  на . Таким образом, в уравнении остались только  и , а  и  исключены:

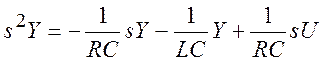                                                                                                                              (19)

В (19) перенесём все слагаемые, содержащие , в левую часть и выполним обратное преобразование Лапласа. При этом операция умножения на  заменится на оператор дифференцирования по времени.

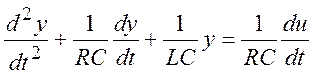                                                                                                                               (20)

Выполним замены  и . Окончательный вид уравнения:

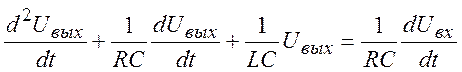                                                                                                                   (21)

Выполнить обратный переход от дифференциального уравнения к системе уравнений состояния может оказаться более трудной задачей, так как требуется ввести новые функции так, чтобы уравнение распалось на систему, в которой в каждом уравнении была бы только первая производная по времени только одной функции, то есть получилась система уравнений типа (3). Более того, для одного и того же уравнения могут быть выбраны различные наборы новых функций. Продемонстрируем на примере уравнения (20) один из способов такого перехода. Для этого перенесём в левую часть слагаемые, содержащие производные, а в правую часть – слагаемое без производной, и в левой части вынесем один оператор дифференцирования:

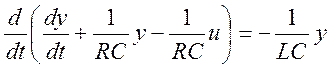                                                                                                                             (22)

Из уравнения (22) видно, каким образом можно выбрать новые функции, чтобы удовлетворить выше написанным условиям. В левой части есть первая производная по времени от скобок, поэтому выражение в скобках обозначим новой функцией:

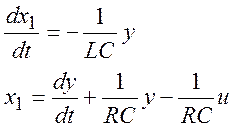                                                                                                                                      (23)

Второе уравнение содержит одно слагаемое с первой производной по времени, поэтому перенесём его в левую часть, а все остальные слагаемые – в правую. То, что стоит под оператором дифференцирования, также обозначим новой функцией, и получим систему из двух уравнений состояния и одно уравнение для выходного параметра:

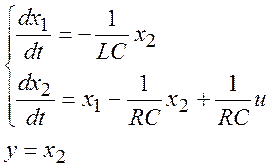                                                                                                                                  (24)

То же самое в матричной форме:

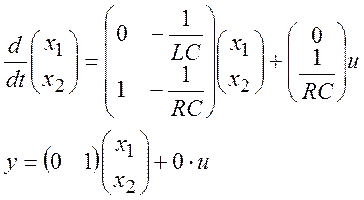                                                                                                                           (25)

Уравнения состояния (25) отличаются от уравнений (17), хотя описывают прохождение сигнала через одну и ту же цепочку (рис. 5). Если в окне параметров блока State-Space заменить матрицы на те, что входят в уравнения (25), результат не изменится, как уже отмечалось выше, могут быть выбраны различные наборы функций.

Пример 3

Рассмотрим случай, когда система имеет несколько входных и выходных параметров (рис. 8).

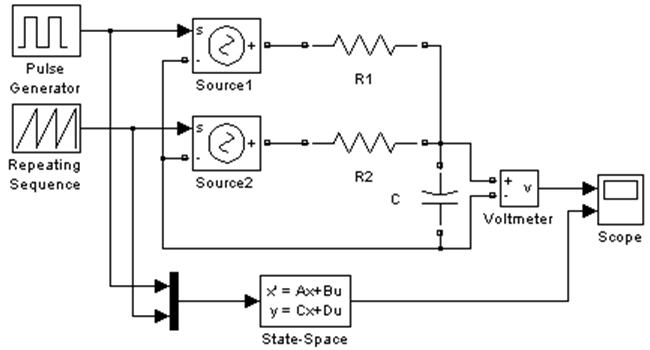
Рис. 8 Система с двумя входными параметрами

В качестве величины, описывающей состояние системы, выбираем напряжение на конденсаторе , первый входной параметр – разность потенциалов, создаваемая первым источником , второй параметр – вторым источником . Уравнения Кирхгофа и закон Ома для цепочки на рис. 8:

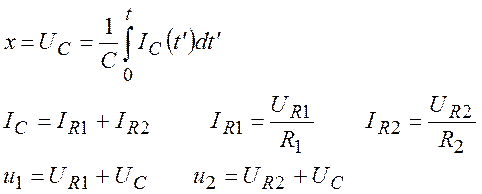                                                                                                                 (26)