Пространство состояний (State-Space). Линейные системы с сосредоточенными параметрами (line and time-invariant system – LTI), страница 4

где , , ,  – токи и падения напряжения на сопротивлениях  и . Исключив из (26) эти токи и напряжения получаем уравнение состояния. Выходным параметром является напряжение на конденсаторе. Уравнения состояния:

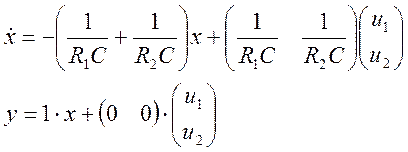                                                                                                                       (27)

В диалоговом окне параметров блока State-Space вводим соответствующие матрицы из (27) рис. 9., а в командной строке задаём переменные

R1 = 1e3;

R2 = 1e4;

C  = 1e-6;

Длительность прямоугольных и треугольных импульсов 0,01с.

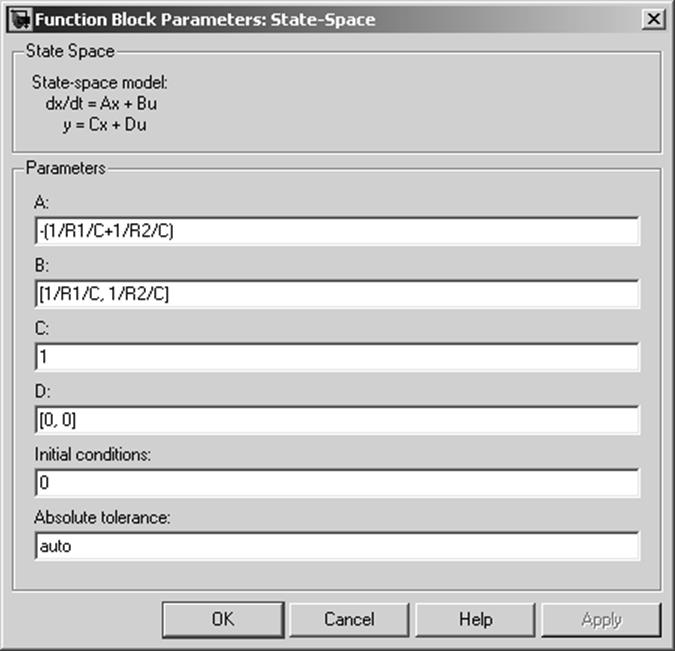
Рис. 9 Параметры State-Space для системы с двумя входными параметрами.

Линейную систему, заданную с помощью четырёх матриц из (5) и (7), можно также задать с помощью передаточной функции (transfer function), если у системы несколько входов, то для каждого входа будет свой коэффициент передачи. В Matlab для того чтобы найти коэффициенты числителя и знаменателя передаточной функции есть функция ss2tf. Первые четыре аргумента – это матрицы A, B, C, D, пятый аргумент – номер входа, соответствующий номеру входного параметра.

Чтобы получить коэффициент передачи интересующего входа линейной системы, к уравнениям (27) применяем преобразование Лапласа:

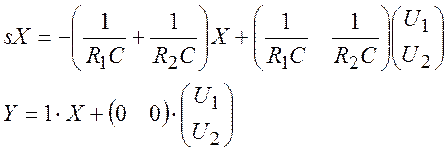                                                                                                                    (28)

где , , ,  Лаплас-образы соответствующих в (27) функций. Из второго уравнения в (28) выразим  через  и подставим в первое уравнение. Если, например, хотим получить коэффициент передачи для первого входа, то надо положить . Это равносильно тому, что мы подключили второй вход к общему проводу, то есть сопротивление  оказалось включённым параллельно вместе с конденсатором. Аналогичные действия для нахождения второго коэффициента передачи. В результате получили два равенства:

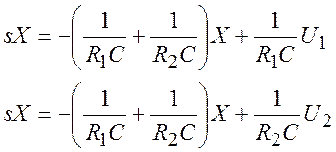                                                                                                                             (29)

В этих выражениях слагаемые с  перенесём в левую часть и приведём подобные. По определению комплексный коэффициент передачи для первого и второго входа:

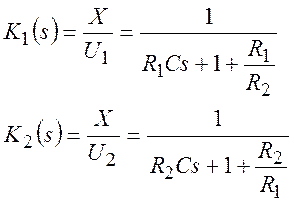                                                                                                                                 (30)

Пример применения функции ss2tf в Matlab для системы показанной на рис. 8, результат сравнивается с формулами (30):

Пример преобразования ss2tf

clear, clc, close all R1 = 1e3;  % сопротивление R1 R2 = 1e4;  % сопротивление R2 C1 = 1e-6; % ёмкость конденсатора C % коэффициенты системы уравнений A = -(1/R1+1/R2)/C1; B = [1/R1, 1/R2]/C1; C = 1; D = [0, 0]; % коэффициенты числителя и знаменателя передаточной функции [b1, a1] = ss2tf(A, B, C, D, 1); [b2, a2] = ss2tf(A, B, C, D, 2); % значения частот в логарифмическом масштабе f = logspace(1, 4, 50); % значения передаточных функций на этих частотах h1 = freqs(b1, a1, 2*pi*f); h2 = freqs(b2, a2, 2*pi*f); % для сравнения вычисляем по формулам k1 = 1./(2*pi*i*f*R1*C1+1+R1/R2); k2 = 1./(2*pi*i*f*R2*C1+1+R2/R1); % АЧХ и ФЧХ с помощью ss2tf figure subplot(2,1,1), semilogx(f, abs(h1),   'b', f, abs(h2),   'g'), grid subplot(2,1,2), semilogx(f, angle(h2), 'b', f, angle(h2), 'g'), grid % АЧХ и ФЧХ по формулам figure subplot(2,1,1), semilogx(f, abs(k1),   'b', f, abs(k2),   'g'), grid subplot(2,1,2), semilogx(f, angle(k2), 'b', f, angle(k2), 'g'), grid

Пример 4

Как уже отмечалось выше, с помощью пространства состояний могут быть описаны не только линейные системы, но и нелинейные, что значительно расширяет класс задач, для которых применим этот метод. В качестве примера рассмотрим амплитудный детектор рис. 10:

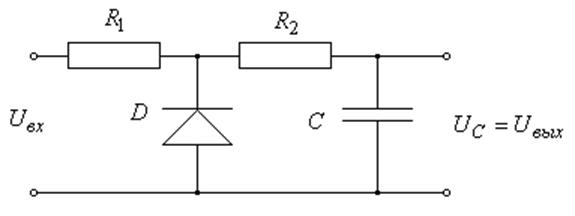
Рис. 10 Схема амплитудного детектора

Для простоты, диод будем считать идеальным ключом, то есть он размыкает цепь, когда на нём положительное напряжение, и замыкает, когда отрицательное. В качестве входного сигнала будем использовать отрезок синусоиды. В Simulink нет специального блока типа State-Space для решения нелинейных задач, поэтому придётся написать свою собственную подсистему, реализующую алгоритм метода. Для сравнения результатов найдём сигнал на выходе с помощью библиотеки SimPowerSystem рис. 11.