Постоянный электрический ток. Плотность электрического тока. Закон Ома для постоянного тока. Линейная электрическая цепь. Джоулева теплота

7. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК. Плотность электрического тока. Закон Ома для постоянного тока. Линейная электрическая цепь. Джоулева теплота.

7.1 Плотность электрического тока. В этом разделе не будем ограничиваться случаем электростатической ситуации и считаем поля, зависящими от времени. Напомним основные понятия, связанные с протеканием тока в проводнике.. Внутренние заряды проводников могут перемещаться под действием приложенного электрического поля. Это движение называется электрическим током. К проводникам относятся металлы, полупроводники, электролиты и ионизованные газы (плазма). Подвижными заряженными частицами в металлах и полупроводниках являются электроны, ионы неподвижны и составляют ионный остов. Электропроводность электролитов обусловлена ионами. В плазме образование тока происходит за счет движения и электронов и ионов. В медленных процессах существенно движение и тяжелых частиц (ионов) и легких частиц (электронов). Примером могут служить ионно-звуковые и магнитогидродинамические волны. В случае быстрых (высокочастотных) процессов, перемещение ионов в плазме мало сказывается на ее электропроводность.

            Плотность тока является количественной характеристикой тока:

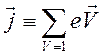                                                ,                                          (7.1)

где суммирование распространяется на все подвижные заряженные частицы в рассматриваемом единичном объеме проводника,  - заряд и направленная скорость частицы. Скорость зарядов зависит от поля, поэтому .

            В отсутствии поля плотность тока равна нулю , так как тепловое хаотическое движение заряженных частиц приводит к нулевой их средней скорости. Если же поле в проводнике отлично от нуля, то возникает направленное движение заряженных частиц и плотность тока отлична от нуля. Под скоростью  в (7.1) будем понимать среднюю направленную скорость движения частиц, тогда при наличии только одного сорта заряженных частиц, формула (7.1) принимает вид

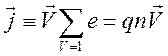                                                ,                               (7.2)

где  - заряд и концентрация заряженных частиц. Если ток создается несколькими сортами заряженных частиц, то в (7.2) необходимо добавить суммирование по ним. Плотность тока связана с плотностью зарядов  уравнением непрерывности (законом сохранения заряда)

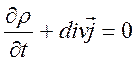                                                .                                    (7.3)

            Сила тока, проходящего через поверхность , представляет собой поток плотности тока через эту поверхность

                                    ,

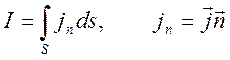где  - единичная внешняя нормаль к поверхности .

7.2. Закон Ома для постоянного тока. Согласно уравнению непрерывности (7.3), постоянному току соответствует плотность заряда не зависящая от времени. Следовательно, этой ситуации должно соответствовать электрическое поле так же  не зависящее от времени, так как . Ранее было показано, что электростатическое поле в проводнике равно нулю, и постоянный ток под действием такого поля не создается. Существование постоянного тока в проводнике возможно только при наличии неэлектростатических сил (сторонних сил - сторонних источников постоянного тока). Такими источниками могут быть гальванические элементы, аккумуляторы, термоэлементы, динамомашины постоянного напряжения. Не вникая в механизмы действия этих источников, введем их чисто формально (феноменологически). Суммарная напряженность электрического поля  в проводнике в рассматриваемой ситуации имеет вид

                                                ,

где  - электростатическое поле, 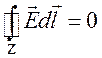,  - напряженность поля сторонних сил. Ограничиваясь рассмотрением слабых полей (линейное приближение), для изотропных проводников будем иметь линейную локальную связь между плотностью тока и полным полем в проводнике (закон Ома)

                                                ,

где  - удельная электропроводность проводника. Соответствующее обобщение на случай анизотропного проводника имеет вид

                                                .

Удельная электропроводность в системе СИ выражается в сименсах на метр ().

            Конечное значение поля  в проводнике не приводит к непрерывному ускорению заряда за счет потерь (диссипации), благодаря различным механизмам (примером может быть сила трения из – за упругих соударений). Рассмотрим закономерность образования постоянного тока при . Уравнение движения заряженной частицы с учетом силы трения запишем в виде

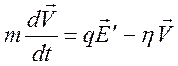                                    ,                                         (7.4)

где  - коэффициент трения. Возможен учет и других диссипативных факторов в (7.4) (например силы вязкости). Общее решение уравнения (7.4) имеет вид