![]() ,
,
где
![]() - постоянная интегрирования. Если
- постоянная интегрирования. Если ![]() , то тогда
, то тогда ![]() и
справедливо представление
и
справедливо представление
![]() .
.
С
течением времени скорость частицы увеличивается и стремится к предельному
конечному постоянному значению ![]() . Время
. Время ![]() называется временем релаксации. Так
как в предельном установившемся состоянии
называется временем релаксации. Так
как в предельном установившемся состоянии ![]() и
имеет место закон Ома
и
имеет место закон Ома ![]() , то получаем формулу для
удельной электропроводности
, то получаем формулу для
удельной электропроводности
![]() .
.![]()
Здесь был проанализирован простейший механизм установления закона Ома в проводящей среде.
7.3.
Линейная электрическая цепь. Выясним
связь между силой тока и и сторонней силой в линейном проводнике, размеры
сечения которого малы по сравнению с длиной В такой модели можно считать
плотность тока постоянной по поперечному сечению проводника. Из закона
сохранения заряда следует постоянство силы тока в каждом сечении проводника.
Таким образом, плотность тока будет изменяться обратно пропорционально площади
поперечного сечения проводника ![]() . Возникает аналогия со
стационарным потоком несжимаемой жидкости в трубе (плотность потока обратно пропорциональна
площади сечения трубы). Закон Ома
. Возникает аналогия со
стационарным потоком несжимаемой жидкости в трубе (плотность потока обратно пропорциональна
площади сечения трубы). Закон Ома ![]() представляет собой
локальное соотношение, поэтому
представляет собой
локальное соотношение, поэтому ![]() является функцией
координаты вдоль осевой линии проводника (
является функцией
координаты вдоль осевой линии проводника (![]() разное
в различных сечениях проводника). Введем в рассмотрение понятие удельное
электрическое сопротивление проводника:
разное
в различных сечениях проводника). Введем в рассмотрение понятие удельное
электрическое сопротивление проводника: ![]() .
Векторный элемент длины проводника
.
Векторный элемент длины проводника ![]() параллелен вектору
плотности тока, поэтому справедливы соотношения
параллелен вектору
плотности тока, поэтому справедливы соотношения
![]() ,
, ![]()
![]() ,
,
где
интегрирование ведется вдоль всего замкнутого проводника, ![]() - электродвижущая сила (э.д.с.),
- электродвижущая сила (э.д.с.), ![]() - электрическое сопротивление
проводника (сопротивление выражается в омах
- электрическое сопротивление
проводника (сопротивление выражается в омах ![]() ).
Соотношение
).
Соотношение ![]() называется законом Ома для всего
замкнутого проводника (закон Ома для электрической цепи).
Электродвижущая сила представляет собой циркуляцию суммарного поля
называется законом Ома для всего
замкнутого проводника (закон Ома для электрической цепи).
Электродвижущая сила представляет собой циркуляцию суммарного поля ![]() , где
, где ![]() -
электростатическое поле (оно потенциально и
-
электростатическое поле (оно потенциально и ![]() ).
Значит, электродвижущая сила это циркуляция стороннего поля вдоль замкнутого
проводника (вдоль токовой линии)
).
Значит, электродвижущая сила это циркуляция стороннего поля вдоль замкнутого
проводника (вдоль токовой линии)
![]() .
.
Электродвижущая
сила отлична от нуля только при условии, что ![]() непотенциальное
поле. Электродвижущую силу можно интерпретировать как работу сторонних сил при
перемещении положительного единичного заряда вдоль замкнутой токовой линии.
Размерность э.д.с. это вольты.
непотенциальное
поле. Электродвижущую силу можно интерпретировать как работу сторонних сил при
перемещении положительного единичного заряда вдоль замкнутой токовой линии.
Размерность э.д.с. это вольты.
Если
цепь состоит из отдельных последовательно соединенных проводников с различными
удельными сопротивлениями ![]() , различными длинами
, различными длинами ![]() и поперечными сечениями
и поперечными сечениями ![]() (Рис. 7.1, здесь заштрихованный кружок
обозначает источник э.д.с.), то сопротивление всей цепи есть сумма всех
сопротивлений
(Рис. 7.1, здесь заштрихованный кружок
обозначает источник э.д.с.), то сопротивление всей цепи есть сумма всех
сопротивлений
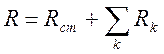 ,
, ![]() ,
,
где
![]() - внутренне сопротивление источника э.д.с.
- внутренне сопротивление источника э.д.с.
7.4.
Джоулева теплота. Протекание
постоянного тока обеспечивается сторонними силами неэлектростатического
(точнее сказать непотенциального) происхождения. Как было показано в разделе
7.2, равномерность движения заряженных частиц обеспечивается диссипативными
механизмами, приводящими к торможению частиц и к установлению стационарного
состояния. В разных проводниках механизмы торможения различны, ограничимся
здесь учетом влияния простейшей силы трения (раздел 7.2) ![]() , где
, где ![]() -
коэффициент трения и скорость заряженной частицы. Уравнение движения имеет вид
(7.4)
-
коэффициент трения и скорость заряженной частицы. Уравнение движения имеет вид
(7.4)
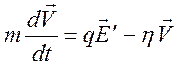 ,
,
равномерное движение осуществляется при
![]() .
.
Работа
![]() силы
силы ![]() над
частицей за время
над
частицей за время ![]() на пути
на пути ![]() имеет
вид
имеет
вид
![]() .
.![]()
Работа
силы трения равна количеству теплоты, получаемой окружающей средой. При
равномерном движении ![]() работа
работа ![]() ,
совершаемая силой
,
совершаемая силой ![]() , полностью переходит в теплоту,
выделяемую в проводнике. Отнесенная к одной частице эта теплота равна
, полностью переходит в теплоту,
выделяемую в проводнике. Отнесенная к одной частице эта теплота равна ![]() . В единичном объеме выделится теплота
. В единичном объеме выделится теплота
![]() ,
,
где
![]() - концентрация заряженных частиц. При
учете представлений
- концентрация заряженных частиц. При
учете представлений ![]() , получаем
, получаем ![]() , и теплота, выделяемая в единичном объеме
за
, и теплота, выделяемая в единичном объеме
за
время
![]() (джоулева теплота) имеет вид
(джоулева теплота) имеет вид
![]() ,
,
в
проводнике в объеме ![]() за время
за время ![]() выделится
теплота
выделится
теплота
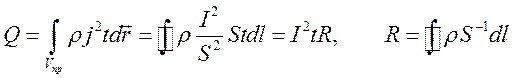 .
.
За одну секунду выделится теплота
![]() ,
,
эта
величина выражается в ваттах ![]() .
.
Пусть в замкнутой цепи действует источник с э.д.с. ![]() и сопротивление проводника, подключенного
к этому источнику
и сопротивление проводника, подключенного
к этому источнику ![]() . Ток находится из выражения
. Ток находится из выражения ![]() . Количество теплоты, выделенное за одну
секунду в проводнике и в источнике
. Количество теплоты, выделенное за одну
секунду в проводнике и в источнике
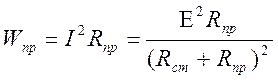 ,
, 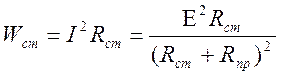
и суммарное количество теплоты имеет вид
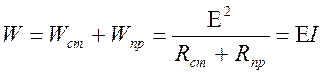 .
.
Отсюда следует, что выделение теплоты обусловлено внешним источником.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.