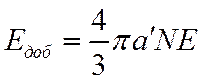 (**)
(**)
Обоснование этого.
Рассмотрим модель вещества, состоящего из абсолютно жестких диполей, в которой отсутствует упругая поляризация.
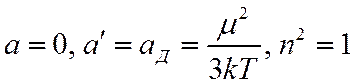 (***)
(***)
Подставляя (***) и (**) в (*), получим
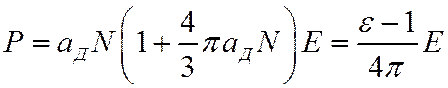
Если рассмотреть два предельных случая слабо и сильно полярных веществ, то для первого случая получим
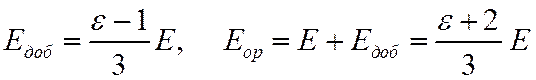
что совпадает с полученной ранее ф-лой для слабополярных диэлектриков и дает хорошее соответствие с экспериментом.
Для сильно полярных диэлектриков получается
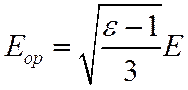
Это поле с ростом диэлектрической проницаемости растет медленнее, чем у Дебая.
Без вывода
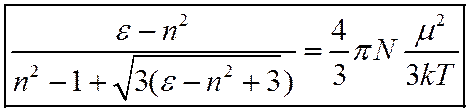
Хорошее согласование с экспериментом в широком диапазоне
изменения ![]() .
.
Поляризация в переменном поле. Теория Дебая. Дисперсионные свойства диэлектриков.
Процессы при включении и выключении постоянного поля. Большинство релаксационных процессов описывается уравнением
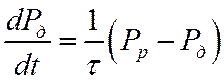
где ![]() – равновесная поляризация и
мгновенное значение дипольной поляризации,
– равновесная поляризация и
мгновенное значение дипольной поляризации, ![]() – время
релаксации.
– время
релаксации.
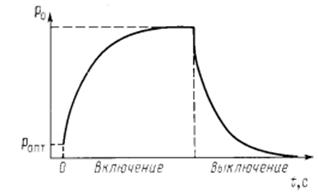
При выключении поля
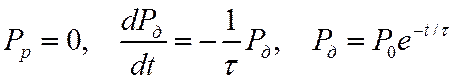
При включении поля
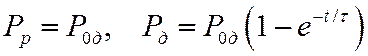
Пусть к диэлектрику приложено переменное поле
![]()
Поляризация будет изменяться
![]()
На низких частотах поляризация равна сумме упругой поляризации, возникающей из-за смещения электронов и ядер, и равновесной дипольной поляризации:
![]()
Было:
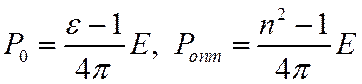
Тогда равновесная дипольная поляризация для заданного значения напряженности поля
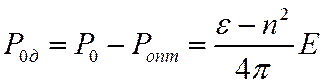
Уравнение для мгновенного значения дипольной поляризации
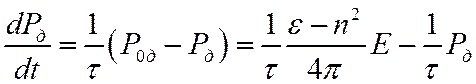
Или
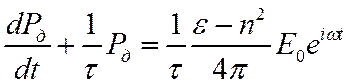
Его решение
![]()
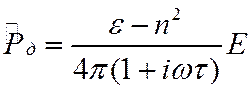
Найдем диэлектрическую проницаемость в переменном поле.
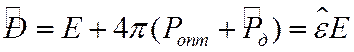
После преобразований
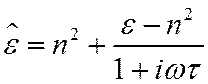
Выделим вещественную и мнимую часть у диэлектрической поляризации
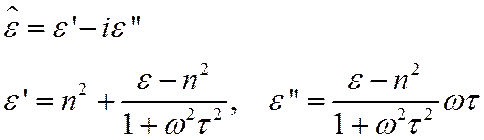
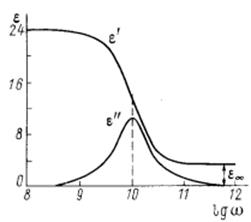
Рассмотрим два предельных случая ![]() .
.
В первом случае ![]() . Во втором случае
. Во втором случае ![]()
![]() .
.
Определим положение максимума. Положим ![]() .
.
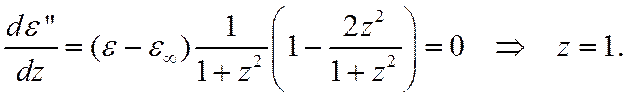
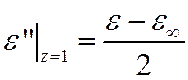
На этой частоте
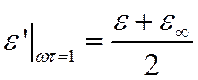
Покажем, что мнимая часть диэлектрической проницаемости отвечает за потерю энергии в переменном поле. Заполним конденсатор диэлектриком и подадим на него переменное напряжение. Определим заряд и ток.
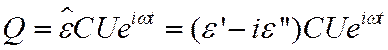
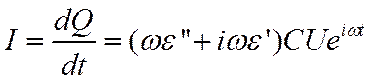
Первое слагаемое соответствует току проводимости,
протекающему по эквивалентному сопротивлению 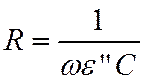 . На
нем выделяется мощность
. На
нем выделяется мощность
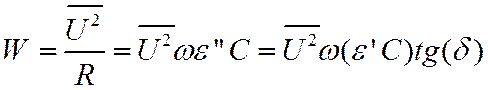
![]() – вещественная часть емкости.
– вещественная часть емкости.
Кривые Коул-Коула
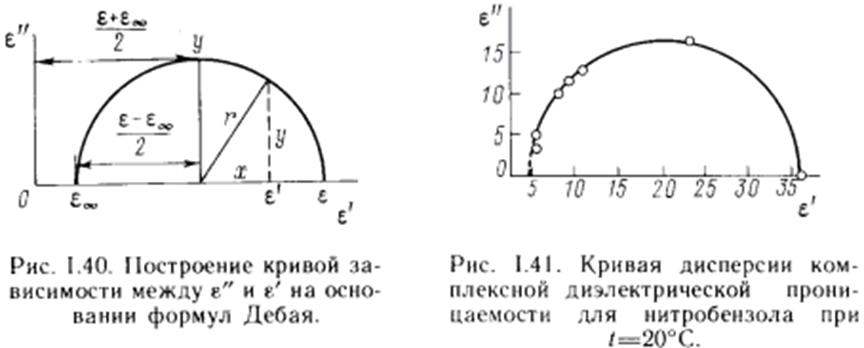
Покажем, что кривая ![]() есть
полуокружность радиуса
есть
полуокружность радиуса ![]() . Для этого перейдем в
систему координат (x, y), где
. Для этого перейдем в
систему координат (x, y), где
![]()
Подставим полученные выражения для ![]()
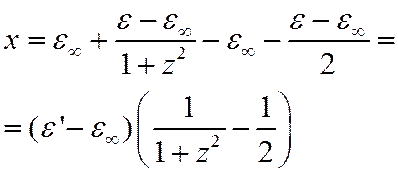
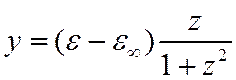
Получим уравнение окружности
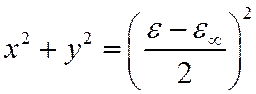
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.