![]() – оптическая диэлектрическая
проницаемость,
– оптическая диэлектрическая
проницаемость, ![]() – поляризуемость молекулы в
оптическом диапазоне. Молярная поляризация переходит в рефракцию
– поляризуемость молекулы в
оптическом диапазоне. Молярная поляризация переходит в рефракцию
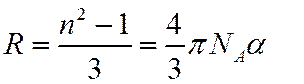 .
.
Величины ![]() и
и ![]() близки по величине. Их различие связано с
существованием двух механизмов упругой поляризации: смещения эл. облаков
относительно положительных зарядов и смещение атомов др. относительно друга. В
оптическом диапазоне второй механизм влияет меньше. Всегда
близки по величине. Их различие связано с
существованием двух механизмов упругой поляризации: смещения эл. облаков
относительно положительных зарядов и смещение атомов др. относительно друга. В
оптическом диапазоне второй механизм влияет меньше. Всегда ![]() . Считая
. Считая ![]() можно
определять
можно
определять ![]() , измеряя П и R при одной и той же температуре
, измеряя П и R при одной и той же температуре 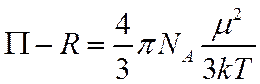 –
способ определения дипольного момента по поляризации паров вещества.
–
способ определения дипольного момента по поляризации паров вещества.
Поляризация конденсированных диэлектриков.
Теория Дебая.
Неполярные диэлектрики.
Нужно учитывать не только вш. поле, но и поле соседних молекул.
Приближение: молекулы точечные, поле, действующее на молекулу постоянно.
![]()
Метод Лоренца.
Используется понятие внешнего (среднего) и локального поля.
Внешнее поле – это поле, приложенное по всему объему диэлектрика, характеризуется средней напряженностью электрического поля:
![]()
Внешнее поле создается зарядами вне диэлектрика (например, на обкладках конденсатора) и связанными зарядами на поверхности диэлектрика.
Локальное поле – поле, действующее на конкретную данную молекулу диэлектрика:
![]()
![]() – поле, созданное
молекулами диэлектрика, окружающими данную молекулу.
– поле, созданное
молекулами диэлектрика, окружающими данную молекулу.
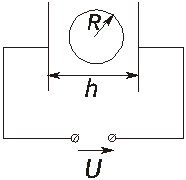
Найдем ![]() , для этого мысленно
окружим рассматриваемую молекулу сферой радиуса R много большей молекулы.
В то же время сама эта сфера должна быть намного меньше толщины рассматриваемого
диэлектрика h.
, для этого мысленно
окружим рассматриваемую молекулу сферой радиуса R много большей молекулы.
В то же время сама эта сфера должна быть намного меньше толщины рассматриваемого
диэлектрика h.
Разделим ![]() на две составляющие:
на две составляющие:
![]()
где ![]() –
поле, действующее на данную молекулу, создаваемое молекулами, находящимися за
сферой, так называемое поле дальнего окружения;
–
поле, действующее на данную молекулу, создаваемое молекулами, находящимися за
сферой, так называемое поле дальнего окружения;
![]() – поле,
создаваемое молекулами, находящимися внутри сферы – поле ближнего окружения.
– поле,
создаваемое молекулами, находящимися внутри сферы – поле ближнего окружения.
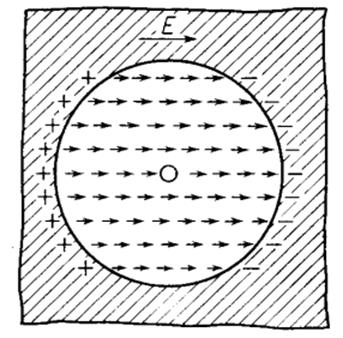
Определим Е1. Для этого мысленно извлечем шар радиуса R из диэлектрика и рассмотрим получившуюся полость отдельно.
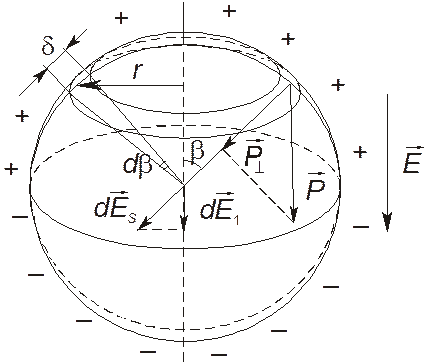
Рис. 18. Сферическая полость в диэлектрике
Выделим на сфере элементарную площадку шириной d и площадью dS как показано на рис. 18.
В целом на площадке имеется связанный поверхностный элементарный заряд
dq = sdS,
где s – плотность поверхностного связанного заряда на dS.
Плотность поверхностного связанного заряда у диэлектриков равна модулю нормальной составляющей вектора поляризации. Таким образом, можно записать:
s = Р^ = Рcosb.
Элементарный заряд dq создает в центре сферы элементарную напряженность:
dE1 = dES cosb.
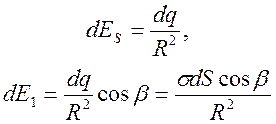
dS = 2prd = 2p(Rsinb)d = 2pR2sinbdb.
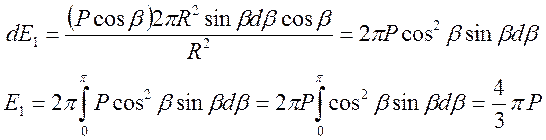
Для неполярных диэлектриков напряженность поля ближнего окружения E2 практически равна нулю: E2 » 0. Покажем это.
Поле ближнего окружения может быть определено как сумма полей молекулярных диполей внутри сферы
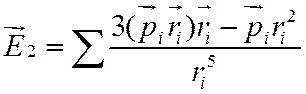
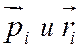 – дипольный момент
молекулы и ее расстояние от центра сферы.
– дипольный момент
молекулы и ее расстояние от центра сферы.
Это поле для неполярных молекул может быть вычислено для случая, когда молекулы образуют правильную кубическую решетку.
Будем считать индуцированные дипольные моменты всех молекул одинаковыми. Выберем декартову СК. Напишем проекции поля на оси.
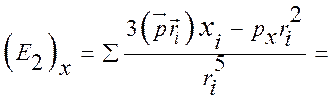
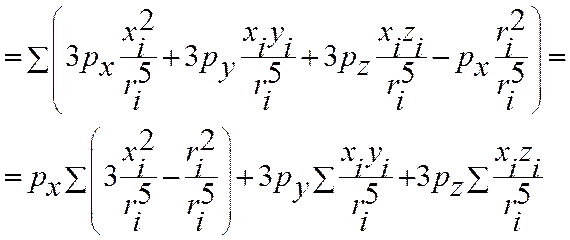
Аналогичные
выражения можно записать для 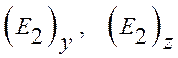 .
.
Для рассматриваемого случая решетка обладает тремя осями симметрии четвертого порядка. Т.е. должны выполняться равенства
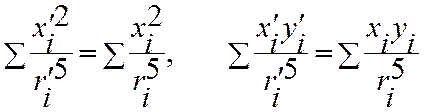 (*)
(*)
где ![]() – координаты молекул
при повороте сферы вокруг любой из осей на 90о.
– координаты молекул
при повороте сферы вокруг любой из осей на 90о.
Например, при повороте вокруг оси Z
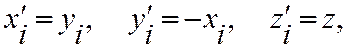
поэтому
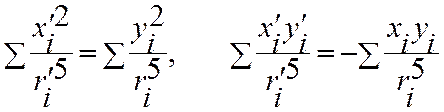 (**)
(**)
Сравнивая (*) и (**), получим
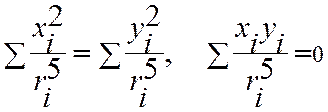
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.