Проведя аналогичные рассуждения для поворота сферы относительно других осей, получим
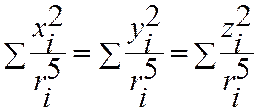
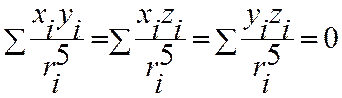
Из первого соотношения можно записать
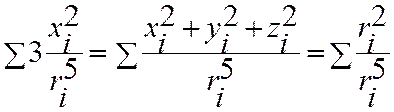
Подставив это в 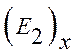 ,
получим, что
,
получим, что 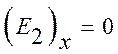 . Аналогично – для других компонент.
Т.о.,
. Аналогично – для других компонент.
Т.о., ![]() .
.
Следовательно, локальное поле Лорентца для неполярных диэлектриков с правильной кубической решеткой.
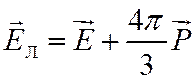 , (1)
, (1)
Аналогично – для неполярных жидких и аморфных тел, где молекулы расположены хаотически.
В этом случае суммирование заменяется усреднением
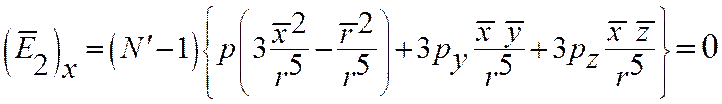
![]()
Уравнение (1) устанавливает связь между локальным и внешним полем.
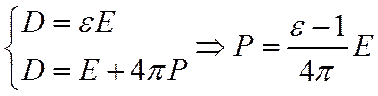 . (2)
. (2)
Подставим (2) в (1):
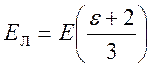 . (3)
. (3)
Уравнение (3) показывает, что напряженность локального поля зависит от материала диэлектрика.
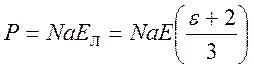 .
.
С учетом выражения (2), получим уравнение Клаузиуса – Мосотти:
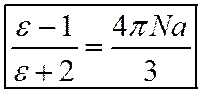 (4)
(4)
Уравнение Клаузиуса – Мосотти справедливо только для неполярных диэлектриков (т. е. учитывает только электронную поляризацию). Позволяет устанавливать связь между макроскопическим параметром, характеризующим диэлектрик как непрерывное тело, а именно диэлектрической проницаемостью e и его микроскопическими параметрами: концентрацией молекул N и поляризуемостью молекул a.
Для инженерных расчетов уравнение (4) можно использовать в модифицированном виде:
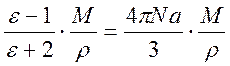
где M – молярная масса вещества;
r – плотность вещества.
Так как, по определению, NM/r – число Авогадро NA, то
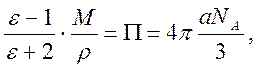
где
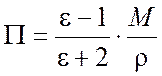 – молярная поляризация.
– молярная поляризация.
Установлено, что для всех неполярных диэлектриков e » n2, где n – коэффициент преломления электромагнитных волн в диэлектрике (ф-ла Лорентц-Лоренца)
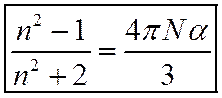
или
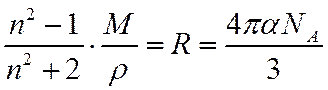
гле
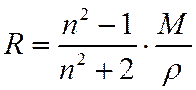 – молярная рефракция.
– молярная рефракция.
Полярные диэлектрики.
Теория Дебая.
Первая теория поляризации полярных диэлектриков была предложена Дебаем. В ее основе – предположение о справедливости для полярных диэлектриков формулы
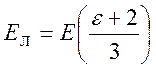 ,
(*)
,
(*)
полученной для неполярных диэлектриков, или для оптических частот
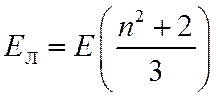
Напишем два выражения для вектора поляризации
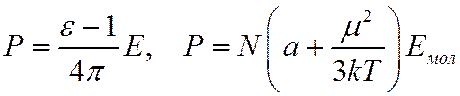
В качестве поля, действующего
на молекулу подставим (*) ![]() . Тогда
. Тогда
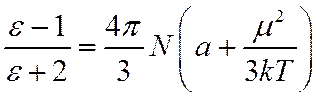
Поляризуемость в постоянном поле можно заменить на оптическую поляризуемость, выраженную из ф-лы Лорентц-Лоренца
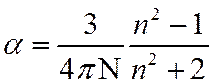
Из двух последних формул получаем
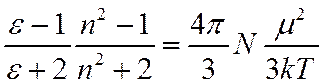
Окончательно ф-ла Дебая имеет вид
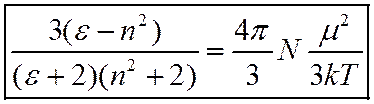
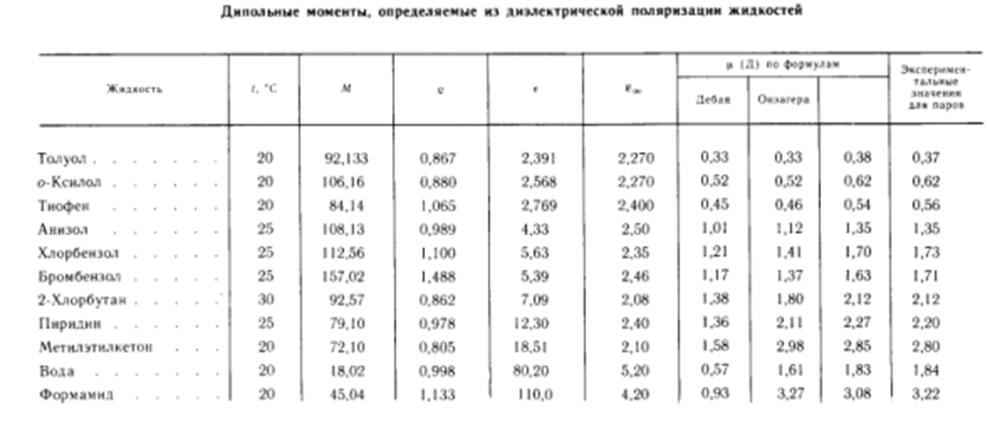
Хорошее соответствие эксперименту дает только для ![]() . Например, для воды измеренное для паров
значение момента
. Например, для воды измеренное для паров
значение момента ![]() Д, а по ф-ле Дебая
Д, а по ф-ле Дебая ![]() Д.
Д.
Теория Онзагера
Уточнение теории Дебая.
Поле, действующее на молекулу, представляется в виде поля сферической полости, вырезанной вокруг молекулы, и т.н. реактивного поля
![]()
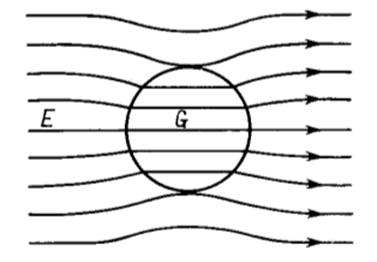
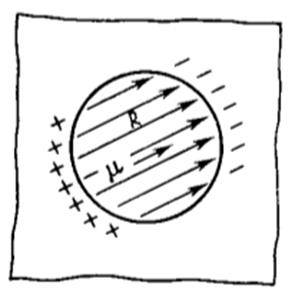
Поле внутри полости однородное, больше, чем в диэлектрике, и сонаправлено с ним
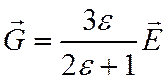
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.