Основы электрогидродинамики. Система уравнений электрогидродинамики (ЭГД). Условия применимости уравнений ЭГД. Невозмущенное состояние

16. Основы электрогидродинамики. Система уравнений электрогидродинамики (ЭГД). Условия применимости уравнений ЭГД. Невозмущенное состояние. Линейное приближение. Классификация ЭГД явлений.

16.1. Система уравнений электрогидродинамики (ЭГД). Электрогидродинамика,

как самостоятельный раздел физики берет свое начало с исследований Остроумова Г.А. (1954). Изучение процессов в электропроводящих средах (газах и жидкостях) в приближении теории сплошной среды основывается на использовании системы уравнений Максвелла и уравнений газовой динамики с учетом действия сил электромагнитной природы. Отличие электрогидродинамических (ЭГД) процессов от магнитогидродинамических (МГД) процессов заключается в том, что в ЭГД процессах плотность энергии магнитного поля пренебрежимо мала по сравнению с плотностью энергии электрического поля:

                                                .

По этой причине в приближении ЭГД делается пренебрежение влиянием магнитного поля. В электрогидродинамике делается пренебрежение релятивистскими эффектами.

Уравнения Максвелла в такой ситуации описывают продольное (потенциальное) электрическое поле. ЭГД волны имеют одну общую черту с ионно – звуковыми волнами: используется приближение потенциального электрического поля. Однако существует принципиальное отличие: ионно – звуковое приближение для плазмы это  двухжидкостное приближение (описывается движение электронов и ионов), а ЭГД приближение это одножидкостное приближение. Как правило, в ЭГД носителями электрических зарядов являются ионы, влияние электронов не существенно. Опишем процесс системой уравнений

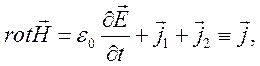
где

,  ,

 - электропроводность среды,  - скорость среды,

,

 - плотность электрических зарядов при движении тяжелых заряженных частиц (ионов). Напомним, что обобщенный закон Ома для медленных нерелятивистских процессов рассматривался в разделе 14.3 при описании МГД процессов, когда плазма рассматривалась как единая среда (в таком рассмотрении делалось пренебрежение плотностью тока ).

Следствием того, что , является уравнение

                                                ,

или эквивалентное представление

                        .

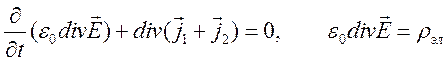Для замыкания системы уравнений используются уравнения динамики несжимаемой электропроводящей жидкости.

            Уравнение непрерывности (сохранения массы) в таком приближении имеет вид

                                                ,        ,           ,

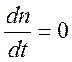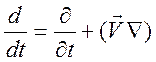 - концентрация ионов.

            Уравнение движения

                                                ,

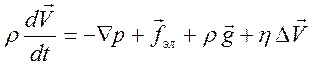где  - плотность среды (масса единицы объема),  - давление,  - ускорение силы тяжести,  - коэффициент вязкости,  - плотность сил электрической природы (используются различные приближения). Представление для плотности силы  будет дано в конце этого раздела.

            Уравнение состояния для давления (используются различные модельные описания)

                                                            ,

где  - температура жидкости.

            Уравнение переноса тепла (уравнение эволюции температуры ) можно получить из уравнения изменения внутренней энергии среды. Если температура среды совпадает с температурой, характеризующей внутренние степени свободы, то тогда средняя энергия частицы дается формулой , где  - теплоемкость при постоянном удельном объеме. Для плотности внутренней энергии среды  ( - концентрация ионов) используем уравнение в интегральной форме

                                                ,

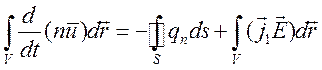где  - произвольный фиксированный объем и поверхность, окружающая этот объем. Для описания потока тепла используем закон Фурье – Ньютона:  - поток тепла,  - коэффициент теплопроводности,  - проекция вектора  на внешнюю к поверхности  нормаль. Уравнение изменения внутренней энергии приводится к виду

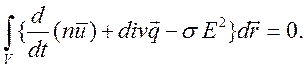
Из произвольности объема  следует равенство нулю подынтегрального выражения. Принимая во внимание уравнение неразрывности 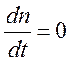, получим уравнение переноса тепла

                                                ,

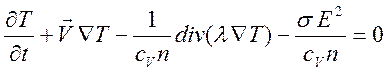где .

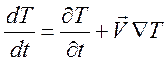            Плотность электрической силы  в одном из возможных приближений имеет вид