Индивидуальная лавина является первичным и неотъемлемым элементом любого механизма пробоя. Рассмотрим лавину в однородном внешнем поле E0между плоскими электродами. Пусть она начинается от одного электрона, вылетевшего с катода в момент t = 0. Ось хнаправим от этого места катода в сторону анода. Радиальное расстояние от оси хобозначаем r.
Движение электрона в электрическом поле в газе имеет диффузионный характер и сопровождается многочисленными упругими рассеяниями и более редкими соударениями с возбуждением нейтральных атомов (молекул). Процессы ионизации при электрон-атомных соударениях играют наиболее важную роль в лавинообразном размножении электронов, другие соударения являются «помехами» в формировании лавины: на них тратится 70-95 % всей энергии, получаемой электроном от электрического поля между актами ионизации.
Радиальный размер лавины со временем нарастает вследствие диффузии электронов при многократных упругих рассеяниях (рис. 2.3).
|
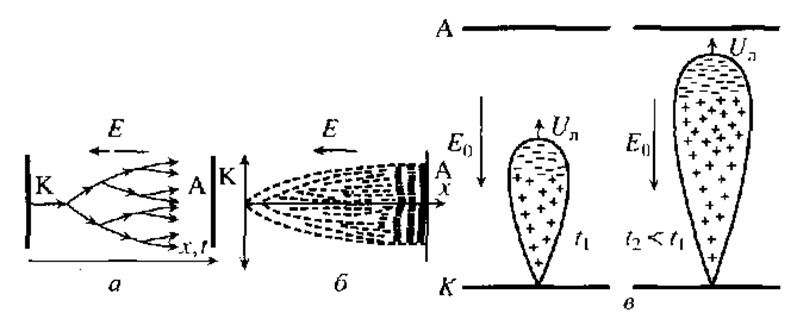
Рис. 9. а — схема лавинного
размножения электронов в промежутке между катодом К и анодом А; б —
схема диффузионного расплывания электронной лавины, которая рождается от
электрона, вышедшего из определенного места катода; в — электронная
лавина — схематические очертания и распределения зарядов r два последовательных момента времени |
Значения коэффициента а определяются сечением ионизации электронным ударом, зависящим от энергии электрона.
Если каждый электрон испытывает до ионизации множество упругих рассеяний, то в электрическом поле устанавливается квазистационарное распределение электронов и а не зависит от х.
Ионизационные коэффициенты а можно определить, используя значения сечений элементарных процессов ионизации, возбуждения, рассеяния, рекомбинации и др. в результате моделирования лавины путем решения кинетического уравнения Больцмана или с помощью метода Монте-Карло.
С учетом возможного образования отрицательных ионов полные числа электронов и ионов нарастают по мере продвижения лавины как
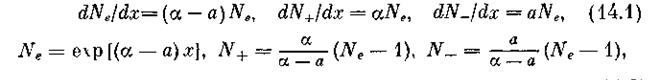
где α и α — коэффициенты ионизации и прилипания. Все нарождающиеся
электроны летят к аноду одной группой со скоростью дрейфа vд = μеΕ0. Однако
вследствие диффузии электронное облако расплывается около центральной точки хо
= vдt, r = 0.
Плотность электронов в облаке пе(х, r, t) подчиняется
общему уравнению диффузии в котором должны быть приняты во
внимание дрейфовое движение и рождение. Решение уравнения имеет
вид 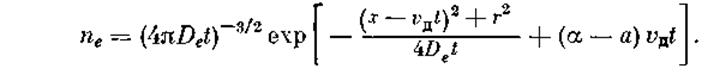
|
где ε — средняя энергия электронов. |
Плотность пе падает
с расстоянием от движущегося центра по гауссову закону. Радиус
сферы, на которой плотность ровно в е раз меньше, чем в центре (плотность
в центре ne{x0, 0, t),растет
с течением времени
(или по мере продвижения лавины) по характерному для диффузии закону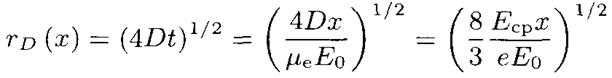
Плотность ионов в отсутствие прилипания в пределе t-> °° и не слишком далеко от оси приближенно определяется выражением:
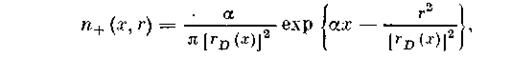
Этот результат имеет наглядный физический смысл. Плотность ионов в следе лавины растет с расстоянием х от катода в соответствии с законом размножения еах. В радиальном же направлении она в каждом сечении х спадает от оси по тому же диффузионному гауссову закону, что и плотность рождающих ионы электронов в тот момент, когда центр электронного облака проходил через данное сечение.
Наряду с ионизацией электроны возбуждают молекулы, которые, как и ионы, остаются практически неподвижными. Пространственное распределение возбужденных частиц, которые, высвечиваясь, могут дать изображение лавины, подобно распределению ионов. Глядя на эту формулу, можно подумать, что видимые очертания лавины примерно совпадают с характерным радиусом распределения rD(x),т. е., что боковой контур лавины имеет параболическую форму r — rD(x)°° Vx, гладко переходя в закругление в области электронной головки лавины. Однако это не так. Каким бы способом не фиксировалось на опыте изображение лавины , граница ее будет соответствовует более или менее определенной абсолютной, а не относительной плотности активных частиц(высвечивающихся молекул, ионов). Величина эта в общем определяется чувствительностью регистрирующей аппаратуры. Поскольку чувствительность подбирается достаточно высокой, минимальная плотность, которая еще регистрируется, гораздо меньше плотности частиц на оси далеко от катода, где ах > 1. Поэтому низкой плотности частиц на видимом контуре лавины rк(х) отвечает небольшое значение показателя экспоненты , гораздо меньше ах. Следовательно, контур соответствует приближенному обращению показателя в нуль и является не параболическим rD~ Vx.а клиновидным:В области головки клин переходит в закругление (рис. 10).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.