
















Часть II. Электродинамика быстропеременных процессов.
10. Описание электромагнитных волн.Волновое уравнение для процесса в однородном изотропном диэлектрике. Плоские волны. Плотность и поток электромагнитной энергии. Уравнения Максвелла для комплексных амплитуд. Диэлектрическая проницаемость при очень больших частотах. Энергетические соотношения для стационарных процессов. Энергия поля в диспергирующих средах. Фазовая и групповая скорости. Различные способы введения понятия групповой скорости. Скорость переноса энергии. Распространение переднего фронта нестационарной волны Теоремы единственности для стационарных задач. Отражение плоских волн от плоской границы раздела. Приближенные граничные условия Леонтовича. Поверхностный импеданс. Потенциалы в электродинамике. Поле точечного и пространственно распределенного источников в однородной среде без дисперсии. Поле короткой линейной антенны. Диполь Герца. Принцип перестановочной двойственности. Дисперсионное уравнение для волн в анизотропной среде. Свойства плоских волн в однородной анизотропной среде. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией. Особенности использования принципа излучения Зоммерфельда для сред с дисперсией. Потенциалы Лиенара – Вихерта. Поле движущегося заряда. Дипольное излучение. Релятивистское излучение.
10.1. Волновое уравнение для процесса в однородном изотропном диэлектрике. Плоские волны. Плотность и поток электромагнитной энергии. Переходя к изучению электромагнитных волн в материальных средах, начнем с волн малой амплитуды (линейное приближение) в однородном изотропном диэлектрике при отсутствии сторонних зарядов и токов
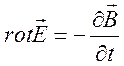 ,
, 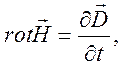
![]() ,
, ![]() .
.
Рассмотрение
начнем с простейшего случая отсутствия пространственной и временной дисперсии: ![]() Используя формулу
Используя формулу
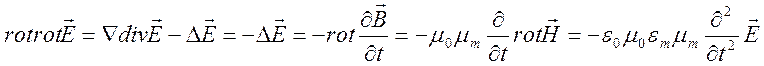
получим волновое уравнение для электрического поля
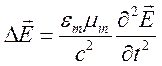 .
.
Аналогичное уравнение получается и для магнитного поля
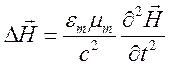 .
.
Эти
волновые уравнения отличаются от волновых уравнений для полей в вакууме только
тем, что в них вместо ![]() входит величина
входит величина 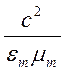 . Отсюда следует вывод, что
электромагнитные волны распространяются в диэлектрике со скоростью
. Отсюда следует вывод, что
электромагнитные волны распространяются в диэлектрике со скоростью 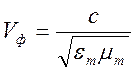 . Как и в вакууме, волны являются поперечными.
. Как и в вакууме, волны являются поперечными.
Рассмотрим плоские монохроматические волны (фурье – образы полей)
![]() .
.![]()
где
![]() - комплексные константы. Для плоской волны
справедливо
- комплексные константы. Для плоской волны
справедливо
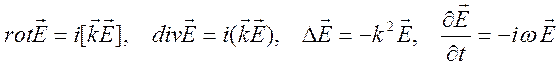 .
.
Волновое уравнение – однородное дифференциальное уравнение в частных производных с постоянными коэффициентами, оно для плоских волн превращается в однородное алгебраическое уравнение. Условие разрешимости последнего дает дисперсионное уравнение
![]() .
.
Отсюда
находим ![]() . Знаки
. Знаки ![]() соответствуют
волнам идущим в противоположные стороны. Фазовая скорость для плоских волн
определяется следующим образом:
соответствуют
волнам идущим в противоположные стороны. Фазовая скорость для плоских волн
определяется следующим образом: 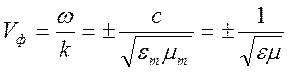 . Волновой вектор
. Волновой вектор ![]() ориентирован в направлении
распространения волны. Рассмотрим одну волну
ориентирован в направлении
распространения волны. Рассмотрим одну волну 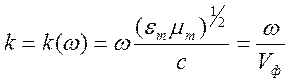 .
Будем иметь представление
.
Будем иметь представление 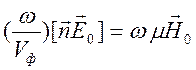 , из которого следует
, из которого следует
![]()
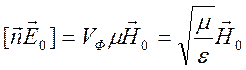 .
.
Аналогично
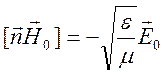 .
.
Оба поля взаимно перпендикулярны и перпендикулярны направлению
распространения волны. Волна является поперечной. Для поперечного поля ![]() справедливо:
справедливо: ![]() , значит
, значит
![]() .
.
Отсюда следует равенство плотностей электрической энергии и магнитной энергии в плоской волне:
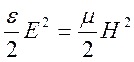 .
.
Вектор плотности потока электромагнитной энергии (вектор Умова -
Пойнтинга) дается формулой ![]() . Для плоской волны это
выражение представляется в виде
. Для плоской волны это
выражение представляется в виде
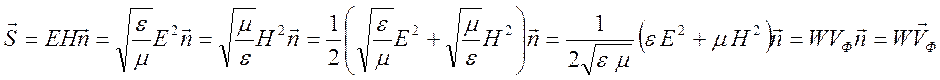 .
.
Где ![]() - плотность электромагнитной
энергии это сумма плотностей энергии электрической и магнитной:
- плотность электромагнитной
энергии это сумма плотностей энергии электрической и магнитной:
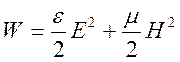 .
.
Значит, можно написать
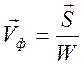 .
.
В среде без дисперсии скорость переноса энергии совпадает с фазовой скоростью. При наличии дисперсии эти скорости различаются.
10.2. Уравнения Максвелла для комплексных амплитуд. Используем систему уравнений Максвелла в материальных средах в следующем виде
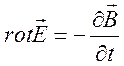 , (10.1)
, (10.1)
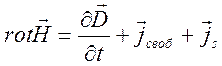 , (10.2)
, (10.2)
![]() , (10.3)
, (10.3)
![]() , (10.4)
, (10.4)
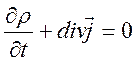 . (10.5)
. (10.5)
В этой системе уравнений число неизвестных функций больше, чем число уравнений, система не замкнутая. Для замыкания системы необходимо добавить уравнения материальных связей, которые в случае линейной электродинамики для немагнитных однородных сред, не изменяющих свои параметры во времени, можно записать следующим образом
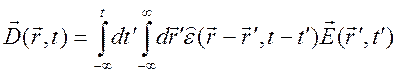 ,
,
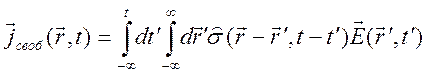 ,
,
![]() .
.
Рассмотрим свойства полей гармонически зависящих от времени
![]() ,
,
что можно записать в другой эквивалентной форме
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.