при этом фурье – образ имеет вид
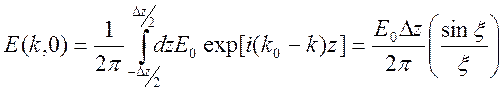 ,
,
где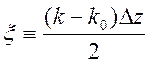 - безразмерный параметр. Функция
- безразмерный параметр. Функция 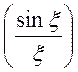 не мала (т.е. порядка единицы) при
не мала (т.е. порядка единицы) при ![]() . Ширина этого интервала составляет
. Ширина этого интервала составляет ![]() . Разброс волновых чисел
. Разброс волновых чисел ![]() , поэтому условие
, поэтому условие ![]() приводится
к виду
приводится
к виду
![]() .
.
Такое же соотношение справедливо для любых квазимонохроматических волновых пакетов. В трехмерных задачах будем иметь
![]() .
.
Если
обозначить ![]() интервал времени, которое пакет проводит в
данной точке пространства (время прохождения пакета через данную точку), то
интервал времени, которое пакет проводит в
данной точке пространства (время прохождения пакета через данную точку), то 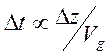 . Поэтому
. Поэтому ![]() . Но
. Но ![]() , где
, где ![]() -
разброс по частотам в пакете. Таким образом, имеем соотношение
-
разброс по частотам в пакете. Таким образом, имеем соотношение
![]() .
.
5). Найдем
связь между групповой скоростью и показателем преломления ![]() (
(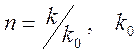 -
волновое число в вакууме). Учтем представление
-
волновое число в вакууме). Учтем представление 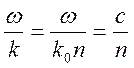 и
продифференцируем соотношение
и
продифференцируем соотношение ![]() :
:
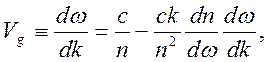
откуда получим
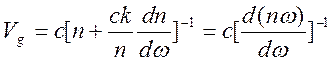 .
.
В
области нормальной дисперсии ![]() . Для большинства сред
(но не для всех) в этой области
. Для большинства сред
(но не для всех) в этой области ![]() , поэтому для них имеют
место неравенства
, поэтому для них имеют
место неравенства ![]() . В области аномальной
дисперсии
. В области аномальной
дисперсии ![]() и при этом
и при этом ![]() может быть очень большим. Групповая
скорость в этой области может быть больше
может быть очень большим. Групповая
скорость в этой области может быть больше ![]() . Но это
конечно, не означает, что какие то участки обгонят передний фронт, движущийся
со скоростью
. Но это
конечно, не означает, что какие то участки обгонят передний фронт, движущийся
со скоростью ![]() . Эти «быстрые» участки при приближении к
фронту тормозятся (при этом в окрестности фронта перестает быть применимым
приближение квазимонохроматичности и теряет смысл понятие групповой скорости)и
они не обгоняют передний фронт. В области аномальной дисперсии групповая
скорость может быть и отрицательной, при этом огибающая перемещается в сторону,
противоположную той, в которую перемещается поверхность равной фазы. В таких
ситуациях понятием групповой скорости нужно пользоваться с большой
осторожностью. При исследовании эволюции поля нужно обратиться к исходному
представлению Фурье (10.10) для волны данного типа и вычислять этот интеграл
нужно по возможности наиболее точными приближенными методами (если интеграл
вычисляется точно, то проблема вообще не возникнет).
. Эти «быстрые» участки при приближении к
фронту тормозятся (при этом в окрестности фронта перестает быть применимым
приближение квазимонохроматичности и теряет смысл понятие групповой скорости)и
они не обгоняют передний фронт. В области аномальной дисперсии групповая
скорость может быть и отрицательной, при этом огибающая перемещается в сторону,
противоположную той, в которую перемещается поверхность равной фазы. В таких
ситуациях понятием групповой скорости нужно пользоваться с большой
осторожностью. При исследовании эволюции поля нужно обратиться к исходному
представлению Фурье (10.10) для волны данного типа и вычислять этот интеграл
нужно по возможности наиболее точными приближенными методами (если интеграл
вычисляется точно, то проблема вообще не возникнет).
6). Рассмотрим
еще один способ введения понятия групповой скорости. Это позволит ввести новые
полезные понятия и позволит придать групповой скорости новый смысл. Пусть
имеется квазимонохроматическое поле вида (ради простоты ограничиваемся случаем
«одномерного» поля ![]() ):
):
![]() , (10.14)
, (10.14)
где
![]() - медленно изменяющаяся огибающая,
- медленно изменяющаяся огибающая, ![]() - быстро осциллирующая, периодическая по
- быстро осциллирующая, периодическая по ![]() функция. В частности, может быть
функция. В частности, может быть ![]() . В предельном случае монохроматического
поля
. В предельном случае монохроматического
поля ![]() - корень дисперсионного уравнения,
описывающий некоторый тип волны,
- корень дисперсионного уравнения,
описывающий некоторый тип волны, ![]() и
и ![]() не зависят от переменных
не зависят от переменных ![]() , в линейных полях
, в линейных полях ![]() и
и
![]() не зависят от амплитуды поля, в нелинейных
полях
не зависят от амплитуды поля, в нелинейных
полях ![]() и
и ![]() зависят
от амплитуды поля (в нелинейных полях понятие нелинейного дисперсионного
уравнения вводится не опираясь на преобразование Фурье. Нелинейным
дисперсионным уравнением, называется условие существования периодического
решения.).
зависят
от амплитуды поля (в нелинейных полях понятие нелинейного дисперсионного
уравнения вводится не опираясь на преобразование Фурье. Нелинейным
дисперсионным уравнением, называется условие существования периодического
решения.).
Для квазимонохромата (10.14) по определению вводятся
понятия локальная частота ![]() и локальное волновое
число
и локальное волновое
число ![]() :
:
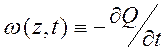 , (10.15)
, (10.15)
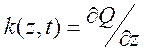 . (10.16)
. (10.16)
В предельном случае монохроматической волны,
определение (10.15), (10.16) дают правильный результат: ![]() ,
,
![]() . Для локальных функций частота и волновое
число можно использовать связь
. Для локальных функций частота и волновое
число можно использовать связь ![]() , существующую для
монохроматической волны (имеется доказательство справедливости этого
утверждения, но здесь приводить его не будем).
, существующую для
монохроматической волны (имеется доказательство справедливости этого
утверждения, но здесь приводить его не будем).
Продифференцируем
(10.15) по ![]() , и (10.16) по
, и (10.16) по ![]() .
Сложение этих результатов дает уравнение, связывающее между собой локальные
функции
.
Сложение этих результатов дает уравнение, связывающее между собой локальные
функции ![]() и
и ![]()
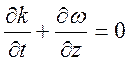 . (10.17)
. (10.17)
Это
очень интересный результат. Уравнение (10.17) это аналог уравнения
неразрывности (закона сохранения). Локальное волновое число ![]() это аналог плотности (плотность волн),
а локальная частота
это аналог плотности (плотность волн),
а локальная частота ![]() это поток (поток волн).
Сразу возникает способ вычисления
это поток (поток волн).
Сразу возникает способ вычисления ![]() : нужно подсчитать число
периодов волны на единице длины. Для нахождения
: нужно подсчитать число
периодов волны на единице длины. Для нахождения ![]() нужно
подсчитать число периодов волны, проходящих через данную точку за единицу
времени. Если в (10.17) использовать связь
нужно
подсчитать число периодов волны, проходящих через данную точку за единицу
времени. Если в (10.17) использовать связь ![]() и
определение групповой скорости
и
определение групповой скорости ![]() , то получим уравнение
в частных производных гиперболического типа для описания эволюции локального
волнового числа
, то получим уравнение
в частных производных гиперболического типа для описания эволюции локального
волнового числа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.