![]() , (10.11)
, (10.11)
где
![]()
![]()
![]()
![]() причем
причем
![]() и
и ![]() .
Формулу (10.11) можно преобразовать к виду
.
Формулу (10.11) можно преобразовать к виду
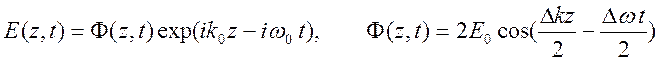 .
.
Множитель
![]() соответствует плоской монохроматической волне
со средними значениями частоты и волнового числа (в радиотехнике такая волна
называется несущей). Функция
соответствует плоской монохроматической волне
со средними значениями частоты и волнового числа (в радиотехнике такая волна
называется несущей). Функция ![]() описывает медленно
изменяющуюся в пространстве и во времени амплитуду этой волны (огибающую).
Частота изменения этой амплитуды
описывает медленно
изменяющуюся в пространстве и во времени амплитуду этой волны (огибающую).
Частота изменения этой амплитуды ![]() . В результате
суперпозиции двух волн близкой частоты возникает периодическое, медленное
изменение амплитуды
. В результате
суперпозиции двух волн близкой частоты возникает периодическое, медленное
изменение амплитуды ![]() и быстрые осцилляции (биение)
(Рис. 10.2). Выясним закономерности перемещения фиксированного значения
амплитуды
и быстрые осцилляции (биение)
(Рис. 10.2). Выясним закономерности перемещения фиксированного значения
амплитуды ![]() или
или ![]() . Так
как
. Так
как ![]() и
и ![]() малы,
то получаем
малы,
то получаем
![]()
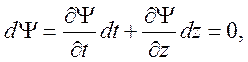
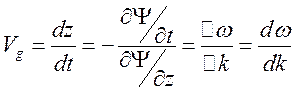
Это означает, что амплитуда биений (огибающая) перемещается со скоростью
![]() ,
,
которая
называется групповой скоростью. Она совпадает с фазовой скоростью только
при отсутствии дисперсии, когда имеется линейная зависимость ![]() от
от ![]() (фазовая
скорость постоянна). Конечно, величине
(фазовая
скорость постоянна). Конечно, величине ![]() можно
придать физический смысл скорости только в том случае, если эта производная
вещественная (допустимо приближенное понимание групповой скорости при слабой
комплексности). В случае комплексности этой производной, эволюция поля
можно
придать физический смысл скорости только в том случае, если эта производная
вещественная (допустимо приближенное понимание групповой скорости при слабой
комплексности). В случае комплексности этой производной, эволюция поля ![]() происходит более сложно, имеет место
«деформация»
происходит более сложно, имеет место
«деформация» ![]() (не происходит перемещения фиксированного
вида профиля ) и это не позволяет ввести понятие огибающей и понятие скорости
перемещения огибающей – групповой скорости. Иногда, чисто формально в такой
ситуации групповой скоростью называют
(не происходит перемещения фиксированного
вида профиля ) и это не позволяет ввести понятие огибающей и понятие скорости
перемещения огибающей – групповой скорости. Иногда, чисто формально в такой
ситуации групповой скоростью называют ![]() ,
однако эта величина не является скоростью перемещения чего - либо (возможны
ситуации
,
однако эта величина не является скоростью перемещения чего - либо (возможны
ситуации ![]() ).
).
4). Рассмотрим более общий случай квазимонохроиатической волны (волновой пакет или цуг волн), когда в суперпозиции участвуют не две волны, а непрерывная совокупность плоских монохроматических волн с узким интервалом частот и волновых векторов:
![]() ,
, ![]() .
.
Это позволяет использовать приближенное представление для (10.10)
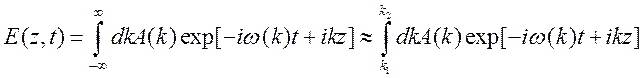 .
.
Такая
ситуация соответствует том, что функция ![]() имеет
резкий максимум при
имеет
резкий максимум при ![]() . Интегрирование в интервалах
. Интегрирование в интервалах ![]() и
и![]() дает
пренебрежимо малый вклад. Используем приближение
дает
пренебрежимо малый вклад. Используем приближение ![]() при
выполнении условия
при
выполнении условия ![]() . В результате, получим
. В результате, получим
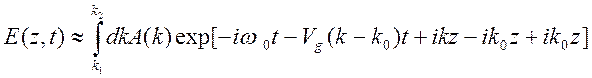 ,
,
![]() (10.12)
(10.12)
где
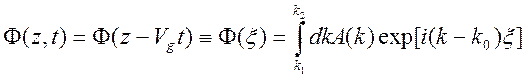 ,
,
где
![]() - значение групповой скорости при
- значение групповой скорости при ![]() ,
, ![]() . Как и
в рассматриваемом в пункте. В случае
. Как и
в рассматриваемом в пункте. В случае ![]() , экспоненциальный
множитель в (10.12) соответствует плоской монохроматической волне со средними
значениями частоты
, экспоненциальный
множитель в (10.12) соответствует плоской монохроматической волне со средними
значениями частоты ![]() и волнового числа
и волнового числа ![]() . Величина
. Величина ![]() описывает
огибающую, которая медленно изменяется в пространстве (на расстояниях порядка
описывает
огибающую, которая медленно изменяется в пространстве (на расстояниях порядка ![]() ) и во времени (с временным масштабом
порядка
) и во времени (с временным масштабом
порядка ![]() ). Огибающая – функция одного переменного
). Огибающая – функция одного переменного ![]() . Это означает, что огибающая переносится в
пространстве с постоянной скоростью, равной групповой скорости для значения
. Это означает, что огибающая переносится в
пространстве с постоянной скоростью, равной групповой скорости для значения ![]() . Волновой пакет (квазимонохромат) движется
как единое целое, без изменения формы. Конечно, этот вывод приближенный, так
как в фурье – представлении использовались только два члена в разложении
. Волновой пакет (квазимонохромат) движется
как единое целое, без изменения формы. Конечно, этот вывод приближенный, так
как в фурье – представлении использовались только два члена в разложении
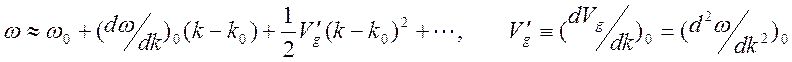 .
.
Оценим
роль отброшенного (третьего) слагаемого, приняв во внимание то, что оно
умножается в показателе экспоненты на время ![]() . Условие
пренебрежения имеет вид
. Условие
пренебрежения имеет вид
![]() , (10.13)
, (10.13)
за
время ![]() пакет проходит расстояние
пакет проходит расстояние ![]() и условие (10.13) можно представить в виде
и условие (10.13) можно представить в виде
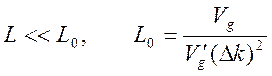 - пространственный масштаб изменения волнового
пакета. На расстояниях больших
- пространственный масштаб изменения волнового
пакета. На расстояниях больших ![]() волновой пакет
претерпевает «искажение» за счет дисперсии, он «расплывается» и здесь понятие
групповой скорости теряет смысл. Выше отмечалось, что понятие групповой
скорости так же теряет смысл при комплексности
волновой пакет
претерпевает «искажение» за счет дисперсии, он «расплывается» и здесь понятие
групповой скорости теряет смысл. Выше отмечалось, что понятие групповой
скорости так же теряет смысл при комплексности ![]() . Это
может быть при наличии диссипации и при распространении волны в «области
непрозрачности» (в этой области производная
. Это
может быть при наличии диссипации и при распространении волны в «области
непрозрачности» (в этой области производная ![]() является
мнимой величиной).
является
мнимой величиной).
Под волновым пакетом понимаем суперпозицию волн с небольшим разбросом волновых векторов. Выясним, какую область в пространстве занимает такой волновой пакет. Рассмотрим простейший пример
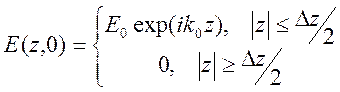 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.