Окислительно-восстановительные электрохимические системы, страница 6

Система электрохимических уравнений сводится здесь к двум уравнениям из числа уравнений систем (3.1) — (3.3) или (2.2) - (2.5):

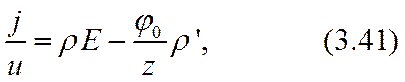
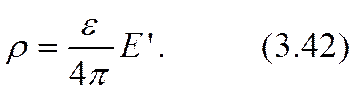
Пусть для определенности дело пойдет о катионах:

Исключение функции r (х) приводит к одному неоднород­ному нелинейному уравнению второго порядка относи­тельно напряженности электрического поля Е:

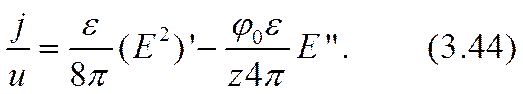
Его первый интеграл имеет вид

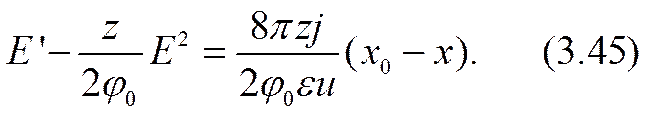
Здесь х₀ означает произвольную постоянную, которая в целях соблюдения общности пока сохраняется неопре­деленной.

Сопоставление размерностей членов уравнения приво­дит к выделению естественной (все коэффициенты уравне­ния становятся единицами) единицы длины L, связанной исключительно со значением плотности протекающего тока j и свойствами электролита: диэлектрической прони­цаемостью e, подвижностью и валентностью ионов u, z, а также температурой опыта Т (через характеристический потенциал j₀ = кТ /е):

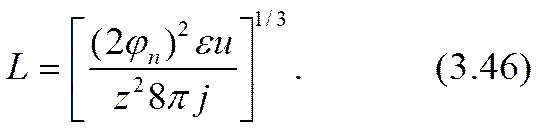
За единицу потенциала целесообразно выбрать значение 2j₀. Тогда естественные единицы нужных величин ока­жутся

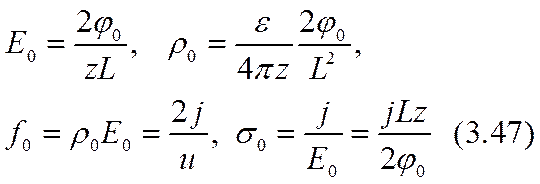
Безразмерные величины примут значения, приводимые здесь для справок:

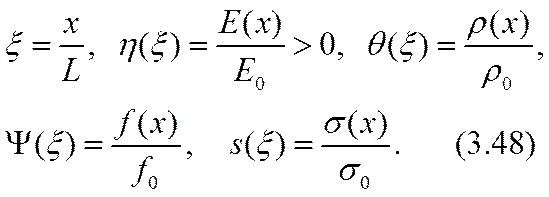
Уравнение (3.45) перепишется в безразмерных перемен­ных:

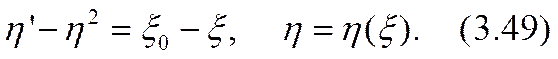
Решение уравнений (3.49) известно [2.17, часть первая, гл. I, § 4, № 4.8, стр. 40; часть третья, гл. I, № 1.13. стр. 295 и гл. II, № 2.162 (II), стр. 401], оно приводится к функциям Бесселя порядка 1/3. Громоздкость этого аналитического решения и его малая обозримость побуж­дают испытать и цифровые методы расчета. Для связи с результатами цифровых расчетов той опорной задачи, которая относилась к бинарному электролиту в системе 1-го рода и изложена в гл. 2, § 2, целесообразно обсудить и унарную задачу в тех же координатах h =h(x).

В качестве примера на рис. 3.3 изображено располо­жение некоторых рассчитанных характерных интеграль­ных кривых в окрестностях начала координат x = 0, h = 0. Из уравнения (3.49) видно, что наклон h' = q (x)  интегральных кривых h =h(x,x₀)имеет одинаковое значение вдоль каждой из парабол

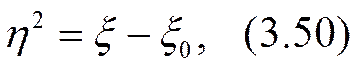
Заметив, что h = 0 при x=x₀, целесообразно точку x=x₀ на оси абсцисс рассматривать как своеобразный «номер» этой параболы. Парабола, отвечающая значению

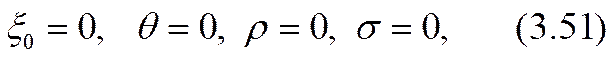
есть геометрическое место точек нулевой плотности заря­дов, т. е. нулевой электропроводности электролита. Из соотношения (3.49) видно, что для каждого избранного фиксированного значения ординаты h(x) = h₀ значение

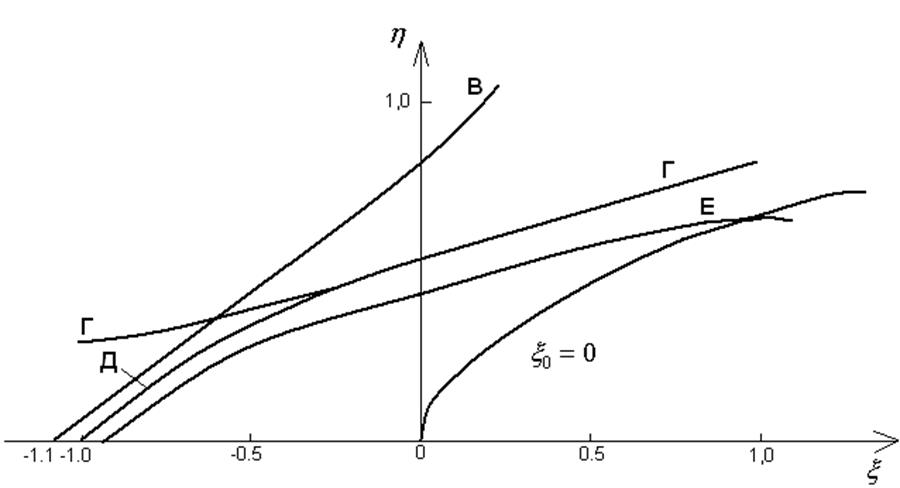
Рис.3.3 Расположение типичных интегральных кривых как решение унарной электродиффузионной задачи. Д – сепаратриса между классами В и Е, Г – геометрическое место экстремальных объемных зарядов.

наклона кривой, т. е. q (x) (плотность объемных зарядов), изменяется линейно с координатой x. Отсюда вытекает, что физический смысл имеет только та часть плоскости h=h(x)  которая расположена левее и выше нулевой параболы x₀ = 0, h(x) ³ 0.

Интегральные кривые типа Е по рис. 3.3 вогнуты к оси абсцисс на всем своем протяжении в области поло­жительных значений напряженности электрического поля, а сама напряженность на них достигает максимальных значений как раз на параболе x₀ = 0, где объемные заряды равны нулю.

Интегральные кривые типа В также имеют участки, где они вогнуты к оси абсцисс. Однако в области высоких значений координаты и напряженности электрического поля они становятся выпуклыми к оси абсцисс. Границей обоих типов кривизны на каждой кривой служит кривая Г, проведенная через точки перегиба всех интегральных кривых. Граничная кривая между типами интегральных кривых Е и В (постоянной и переменной по знаку кривиз­ны), т. е. сепаратриса, изображена кривой Д.