Окислительно-восстановительные электрохимические системы, страница 4

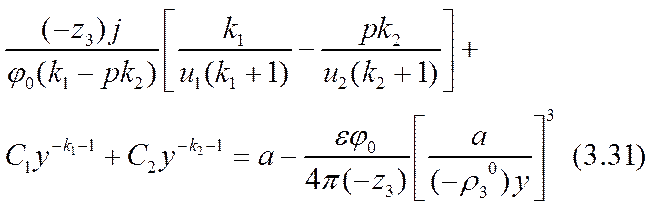
Это уравнение получено в результате использования приближенного значения функции r₃ (х) по формуле (3.26). Поэтому оно само есть уравнение приближенное. Эту приближенность можно использовать для определения констант интегрирования С₁ и С₂, а также масштабного параметра а, усилив «предельное» неравенство (3.26) при соблюдении для r₁ (х) и r₂ (х) условий (3.14)

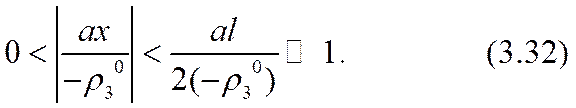
Здесь равенство al = 2 (- r⁰₃ ) соответствовало бы дости­жению «предельного» тока. Усиление (3.32) неравенства (3.26) позволяет обеспечить справедливость точного (а не асимптотического, как в формуле (2.51)) разложения уравнения (3.31) по степеням малого параметра a º a x /(- r⁰₃ ) , |a|<<1. Для определения трех парамет­ров: С₁, С₂ и а достаточно использовать первые три члена этого разложения. Коэффициенты уравнения при нуле­вой, первой и второй степенях разложения окажутся:

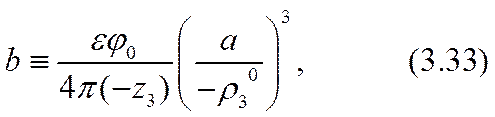
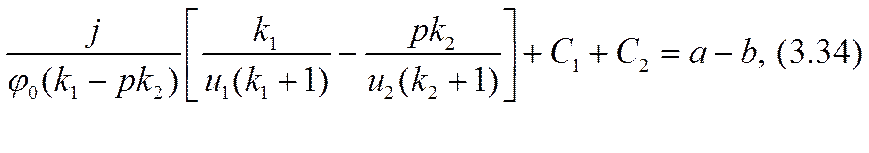
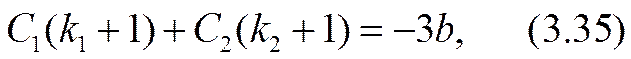
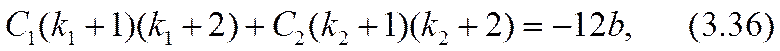
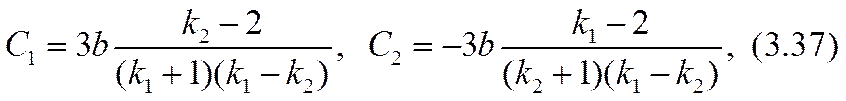
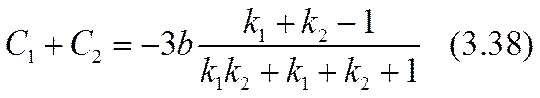
Разрешив эту систему уравнений относительно констант интегрирования и малого масштабного параметра а, можно завершить расчетную задачу в нулевом прибли­жении.

Здесь достаточно ограничиться определением пара­метра а в достигнутом приближении. Для этого нужно исключить из трех уравнений константы интегрирования С₁ и С₂ и составить одно (кубическое) уравнение для параметра а:

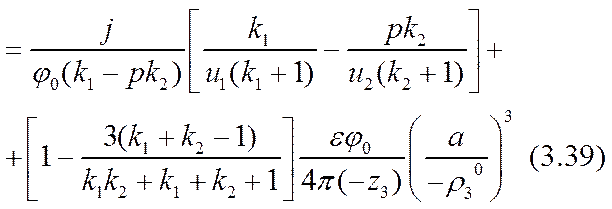
В рамках избранного нулевого (по отступлению от линейности соотношения (3.26), а не по отступлению от электронейтральности!) приближения все условия ана­литической задачи соблюдены точно, кроме закона сохра­нения вещества ионов активных компонент по формуле (3.22). В этом нулевом приближении в замыкающем уравнении (3.31) остались неиспользованные члены со сте­пенями малого параметра а (см. (3.32)) выше второй. Для повышения точности необходимо в линейной форму­ле (3.29) учесть более высокие степени этой малой дроби и подставить полученный результат в уравнение (3.31).

Важнейший результат этого математического анализа явлений в окислительно-восстановительных электрохими­ческих системах состоит в обнаружении в нулевом при­ближении корректной применимости приближения План­ка — точно такой же линейной зависимости плотности распределения пассивной компоненты от координаты r₃ = r₃ (х), как это было установлено для бинарных систем в гл. 2 (формула (2.47)) в первом приближении по отступ­лению от электронейтральности. Поэтому та же самая цепь равенств (2.52) и (2.80), которая в том случае связы­вала все функции с координатой, оказывается справедли­вой и для тернарных систем. В этой цепи важнейшими для физики ЭГД явлений функциями являются объемные заряды r_i ( x), пондеромоторные силы f (х) и созданные ими давления р (х). Что касается следующих приближе­ний, то пока нет оснований утверждать что-либо опреде­ленное ввиду большей сложности явлений в тернарных системах — большого числа необходимых для анализа параметров — по сравнению с бинарными. Было бы полезно продолжить такие исследования и в отношении тернарных и особенно четверных систем.

В работе [3.10] дан пример расчета зависимости важ­нейших электрохимических функций от координаты х для смеси водных растворов иодидов калия при нейтральных электродах в режиме прохождения постоянного тока. Расчет выполнен в приближении линейпого распределе­ния плотности объемного заряда пассивной компоненты К ⁺. Пример соответствует плоскопараллельной ячейке с меж­электродным расстоянием l = 3.2 мм = 3.2• 10^-3 м и пло­щадью каждого электрода 2.56-10^-5 м². Ячейка заполнена водным раствором моноиодида калия в концентрации 0,05 н, в котором добавочно растворен кристаллический иод в концентрации 0,005 н. Здесь символ «н» означает «нормальность» раствора в г-экв/л. Через ячейку прохо­дит постоянный ток плотностью 7.5-10^-8 А/см² = 0,75 А/м² при комнатной температуре 18 °С. Расчет проведен в безразмерных переменных: