4. Несимметричная
линия для уменьшения габаритов свернута в спираль на жестком цилиндрическом
каркасе. Заданное расстояние между проводником и экраном поддерживается за
счет диэлектрической прокладки толщиной 0,45 мм с ![]() .
Если шаг намотки спирали
.
Если шаг намотки спирали ![]() много больше
расстояния между проводом и экраном, то взаимодействие витков спирали
проявится слабо и мы его не учитываем. К тому же, взаимодействие будет
максимально на частотах, когда витки оказываются сфазированными, т.е. когда
на длине витка укладывается длина волны. Для исполь-зуемого макета длина
витка порядка 1 метра (частоты порядка 200 МГц).
много больше
расстояния между проводом и экраном, то взаимодействие витков спирали
проявится слабо и мы его не учитываем. К тому же, взаимодействие будет
максимально на частотах, когда витки оказываются сфазированными, т.е. когда
на длине витка укладывается длина волны. Для исполь-зуемого макета длина
витка порядка 1 метра (частоты порядка 200 МГц).
5. Доступ к линии в произвольном месте реализуется с помощью зонда, цепь которого имеет большое сопротивление и малую емкость. Подключение зонда нарушает однородность линии и приводит к появлению отраженной волны. Однако амплитуда этой отраженной волны достаточно маленькая, что легко проверяется с помощью другого аналогичного зонда.
6. Идеально согласовать линию конечной длины практически невозможно, поэтому отражения от конца линии всегда есть. Несмотря на это, измерения амплитуды и формы падающего импульса можно производить вполне надежно, поскольку при хорошем согласовании на конце линии, амплитуда отраженной волны может составлять единицы процентов от амплитуды падающей. Надо еще учесть, что отраженная волна будет сильно искажена и задержана на время распространения до конца линии и обратно. Если импульс достаточно короткий и измерения проводятся далеко от конца линии, то падающий и отраженный импульсы оказываются разнесенными во времени, не налагаются друг на друга.
7. Следует отметить, что коаксиальная линия тоже позволяет проводить аналогичные измерения. Ее легко свернуть в бухту и можно получить большую длину линии. Однако, для коаксиальной линии чрезвычайно затруднен доступ внутрь линии в произвольном месте, без существенного нарушения ее однородности.
Приложение.
При вычислении
погонных параметров линии мы не будем учитывать, для упрощения задачи, влияние
одного провода на другой, полагая ![]() . Это обстоятельство
позволяет считать, что распределение тока и заряда в каждом проводнике обладает
осевой симметрией. Вычислим сначала емкость и индуктивность единицы длины
линии без потерь, считая проводники идеально проводящими.
. Это обстоятельство
позволяет считать, что распределение тока и заряда в каждом проводнике обладает
осевой симметрией. Вычислим сначала емкость и индуктивность единицы длины
линии без потерь, считая проводники идеально проводящими.
Начнем
с емкости. Пусть полный заряд единицы длины одного провода равен ![]()
(
другого - ![]() ).
Задача сводится к вычислению разности потенциалов проводов. Электрическое
поле одного провода в точке
).
Задача сводится к вычислению разности потенциалов проводов. Электрическое
поле одного провода в точке ![]() на
расстоянии
на
расстоянии ![]() от его оси (смотри рисунок 11 )
от его оси (смотри рисунок 11 ) ![]() . Поле двух проводов в точке
. Поле двух проводов в точке ![]() ,
,
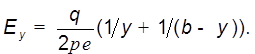 Разность потенциалов
Разность потенциалов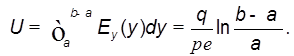
Наконец, емкость 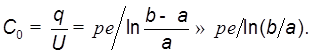 (
1 )
(
1 )
При вычислении индуктивности
единицы длины линии задача сводится к вычислению магнитного потока через
заштрихованную на рис. 11 площадь. Она представляет маленькую часть
длиной ![]() очень
длинного контура с током. Легко по-нять,что провода создают одинаковые потоки,
поэтому достаточно вычислить поток от одного провода и результат удвоить. Магнитная
индукция одного провода с током
очень
длинного контура с током. Легко по-нять,что провода создают одинаковые потоки,
поэтому достаточно вычислить поток от одного провода и результат удвоить. Магнитная
индукция одного провода с током ![]() в
точке
в
точке ![]() на расстоянии
на расстоянии![]() от оси провода, перпендикулярна плоскости площадки
и равна
от оси провода, перпендикулярна плоскости площадки
и равна ![]() Поток
магнитной индукции
Поток
магнитной индукции 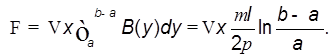
Искомая индуктивность 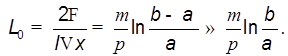 (
2 )
(
2 )
Укажем, для
сравнения, точный результат, который получится с учетом взаимного влияния
проводов. Надо просто заменить аргумент логарифмической функции в формулах
для ![]() и
и ![]() на
следующий:
на
следующий: ![]()
Теперь перейдем к реальным проводникам и вычислим приближенно сопротивле-ние и внутреннюю индуктивность единицы длины линии с учетом скин-ффекта.
Сопротивление считаем следующим
образом. Пока скин-эффект выражен слабо и ![]() , мы его
не учитываем, считая сопротивление, как на постоянном токе. Множи-тель 2
учитывает второй провод.
, мы его
не учитываем, считая сопротивление, как на постоянном токе. Множи-тель 2
учитывает второй провод. ![]() (
3 )
(
3 )
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.