Двухпроводная линия передачи, страница 2

Здесь   - фазовая скорость распространения  волн. Первое слагаемое описывает гармоническое возмущение, распространяющееся по линии со скоростью   в направлении оси .  Постоянная  определяет амплитуду этой волны при    Но,  в целом , амплитуда не постоянна,  а убывает с расстоянием по  мере  распространения  волны по  экспоненциальному  закону за  счет множителя  .  Параметр   называют коэффициентом затухания;  на длине   волна убывает в   раз.  Второе слагаемое представляет аналогичную волну,  бегущую в обратном направлении.                  Пусть линия длиной возбуждается слева (при )  генератором напряжения    с внутренним сопротивлением    и нагружена на конце (при  ) сопротивлением      (рис. 3).  Тогда волну, бегущую от генератора (первое слагаемое в решении) называют прямой или падающей. Другую волну называют отраженной. Отражения могут возникать только в местах  нарушения однородности линии  (конец линии, нагрузка, изгибы, разветвления,  изменения размеров   или    ).  

Определим входное  сопротивление линии и коэффициент  передачи отрезка линии длиной  .

Имеем:                      

На конце линии  .  Подставляя сюда и  , получим соотношение между  и :    Величину    называют коэффициентом отражения от нагрузки (по току). Тогда:

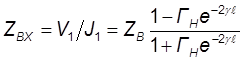                            ,                                                               ( 7 )

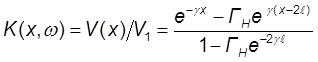                       .                                                   ( 8 ) 

Полезно написать еще формулу, связывающую    и ЭДС генератора   .

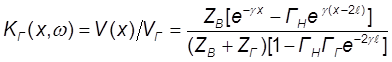                    .                                      ( 9 )

Здесь    - коэффициент  отражения на входе линии,  от генератора.

Если , то линия оказывается идеально согласованной,  и отражений  нет  (бесконечная  однородная линия).  При этом:       и 

                                                                                                              ( 10 ) 

В линии  останется только  падающая волна.  Такую ситуацию мы  прежде всего и рассмотрим.

 Для линии без потерь:   где   - волновое  число среды.  Дисперсии  нет, импульс не ослабляется, не искажается, только запаздывает на время распространения  . При этом волновое сопротивление 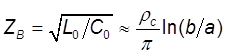  активно и постоянно. Величина   есть волновое  сопротивлениесопротивление среды.  Для вакуума  Ом.

Для линии с потерями параметр   комплексный и зависит от частоты      более сложным образом.  Дисперсия есть,  импульс задерживается, ослабляется и искажается по мере распространения. Частота     входит в параметр     явно,  а также неявно, поскольку сами погонные параметры  ,   и  другие зависят от частоты. Обсудим это подробнее.

Вычисление погонных  параметров линии в широком  диапазоне частот  представляет сложную  электродинамическую задачу по двум причинам.  Первая, это скин-эффект,  который приводит к перераспределению тока по сечению проводников, к "вытеснению" тока к поверхности проводника с ростом частоты. Вторая причина заключается в нарушении осевой симметрии распределения тока и заряда в проводнике,  за счет влияния одного провода  на другой. Например, заряд на поверхности проводника будет неравномерно распределен по периметру. Чем меньше расстояние между проводами, тем сильнее будет выражен этот эффект. 

Нас интересуют прежде всего качественные результаты, и высокая точность не нужна.  Поэтому в приложении  получены приближенные выражения  для погонных параметров линии.  Здесь мы  приведем только результаты с краткими комментариями. 

Обычно потери энергии в проводах больше чем потери окружающей среде. Учтем только первые и положим  . 

Зависимость емкости   от частоты для металлических проводников чрезвычайно слабая  в рассматриваемом диапазоне частот. Не будем ее учитывать и примем             ,  т.е. статической емкости проводов (формула 1 приложения).