Сопротивление
проводников с ростом частоты увеличивается за счет скин-эффекта, поскольку
глубина проникновения поля и тока в проводник уменьшается. При сильно
выраженном скин-эффекте ток убывает экспоненциально по мере удаления от
поверхности проводника. Убывание в![]() раз происходит на
расстоянии
раз происходит на
расстоянии![]() , условно называемом толщиной скинслоя.
Электродинамический расчет дает для этой величины следующее значение:
, условно называемом толщиной скинслоя.
Электродинамический расчет дает для этой величины следующее значение: ![]() ,где
,где ![]() -
удельная проводимость провода, а
-
удельная проводимость провода, а ![]() - его магнитная
проницаемость. В итоге (формулы 3 и 4 приложения):
- его магнитная
проницаемость. В итоге (формулы 3 и 4 приложения):
![]()
![]() (
11 )
(
11 )
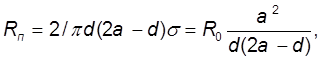
![]()
Таким образом, при
сильном скин-эффекте ( ![]() ) сопротивление
) сопротивление ![]() растет пропорционально
растет пропорционально ![]() .
.
Теперь обратимся к индуктивности. Она определяется или из энергетических соображений, или как коэффициент, связывающий ток в контуре с потоком магнитной индукции, пронизывающим этот контур. Поток индукции реализуется как внутри проводов, так и вне их. Соответственно различают индуктивность внутреннюю и внешнюю.
Внешняя
индуктивность ![]() слабо зависит от распределения
тока внутри проводников и от частоты. Ее можно принять такой, как для
идеальных проводников (формула 2 приложения).
слабо зависит от распределения
тока внутри проводников и от частоты. Ее можно принять такой, как для
идеальных проводников (формула 2 приложения). 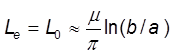 .
.
Внутренняя индуктивность с учетом скин-эффекта такова (формулы 5 и 6 приложения):
![]()
![]() (
12 )
(
12 )

![]()
Для идеально проводящих
проводников внутренняя индуктивность ![]() (поля
внутри нет). К этому мы приходим с ростом частоты и в реальных проводниках,
так как токи вытесняются к поверхности проводников и
(поля
внутри нет). К этому мы приходим с ростом частоты и в реальных проводниках,
так как токи вытесняются к поверхности проводников и ![]() ,
когда
,
когда ![]() (
( ![]() ).
Однако индуктивное сопротивление
).
Однако индуктивное сопротивление ![]() при этом растет, как
при этом растет, как ![]() . Отметим интерес-ный
предельный результат, который легко получается путем разложения выражения для
. Отметим интерес-ный
предельный результат, который легко получается путем разложения выражения для ![]() в ряд при
в ряд при ![]()
![]() , причем всегда
, причем всегда ![]()
Общая
индуктивность ![]() . Соответственно, полное
индуктивное сопротивление
. Соответственно, полное
индуктивное сопротивление ![]() на высоких частотах
растет пропорционально частоте, за счет внешней индуктивности. Поэтому, при
на высоких частотах
растет пропорционально частоте, за счет внешней индуктивности. Поэтому, при ![]() будет выполняется неравенство
будет выполняется неравенство ![]() . Приведенные в табл. 1 и 2 приложения
оценки дают представление о величинах обсуждаемых параметров для медных и
железных проводов.
. Приведенные в табл. 1 и 2 приложения
оценки дают представление о величинах обсуждаемых параметров для медных и
железных проводов.
Теперь мы можем перейти непосредственно к анализу искажений импульса в согласованной линии. Какие искажения импульса следует ожидать? Сначала обсудим это на качественном уровне.
Изображенная на рис. 2 схема отрезка линии малой длины, представляет типичную
ячейку фильтра нижних частот. Вычисления ![]() подтверждают
это. На рис.4 приведены две зависимости
подтверждают
это. На рис.4 приведены две зависимости ![]() от
частоты для отрезков линий длиной 20 и 40 метров с железными проводниками (
от
частоты для отрезков линий длиной 20 и 40 метров с железными проводниками ( ![]()
![]() ). Это типичные
характеристики фильтров нижних частот. Чем длиннее отрезок линии, тем меньше
граничная частота фильтра и тем быстрее убывает
). Это типичные
характеристики фильтров нижних частот. Чем длиннее отрезок линии, тем меньше
граничная частота фильтра и тем быстрее убывает ![]() с
частотой. Для медных проводников затухание значительно меньше, поэтому в
указанном диапазоне частот и расстояний, оно проявляется еще очень слабо.
с
частотой. Для медных проводников затухание значительно меньше, поэтому в
указанном диапазоне частот и расстояний, оно проявляется еще очень слабо.
Пусть на
входе линии мы имеем прямоугольный импульс длительности ![]() (рис. 5). При малой длине линии искажения
будут очень похожи на искажения импульса в инте-грирующей цепочке, при
условии, что постоянная времени цепочки меньше или порядка длительности
импульса ( кривая
(рис. 5). При малой длине линии искажения
будут очень похожи на искажения импульса в инте-грирующей цепочке, при
условии, что постоянная времени цепочки меньше или порядка длительности
импульса ( кривая ![]() ). По мере увеличения длины
линии, длительность фронтов будет расти (граничная частота фильтра
убывает), а резкие изменения (изло-мы) будут становиться более плавными
(гладкими), как для двух, трех-звенной интегри-рующей цепи (
). По мере увеличения длины
линии, длительность фронтов будет расти (граничная частота фильтра
убывает), а резкие изменения (изло-мы) будут становиться более плавными
(гладкими), как для двух, трех-звенной интегри-рующей цепи (![]() ). Аккуратные вычисления целиком
подтверждают эти качествен-ные соображения.
). Аккуратные вычисления целиком
подтверждают эти качествен-ные соображения.
Напомним алгоритм
спектрального метода. Спектр входного прямоугольного импульса с
"амплитудой" ![]() и длительностью
и длительностью ![]() хорошо известен:
хорошо известен: ![]()
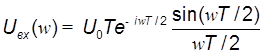 .
.
Коэффициент передачи ![]() отрезка согласованной линии мы
определили. Тогда, спектр сигнала в линии получается перемножением этих
функции.
отрезка согласованной линии мы
определили. Тогда, спектр сигнала в линии получается перемножением этих
функции. ![]() . Наконец, сам сигнал
. Наконец, сам сигнал 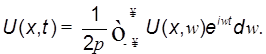
Все сводится к вычислению этого интеграла Фурье.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.