











Z-преобразование
ГУТ 28
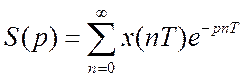
Для ЦС вместо ДПЛ чаще используют Z-П
![]()
Прямое Z-П функции ![]() называется преобразование
называется преобразование

![]() - оригинал, решетчатая функция,
- оригинал, решетчатая функция,
![]() - z-изображение.
- z-изображение.
z-преобразование справедливо только в области абсолютной сходимости ряда
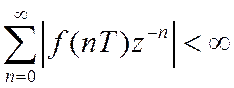
![]() - комплексная величина:
- комплексная величина:
![]()
или
![]()
Условие сходимости
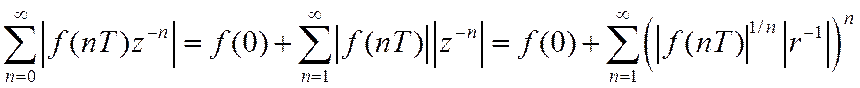
т.к. 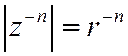 .
.
Ряд сходится, если 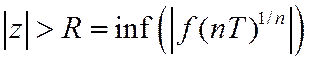 .
.
Например, для ![]() ряд сходится вне
окружности
ряд сходится вне
окружности ![]()
Область сходимости.
Радиус сходимости.
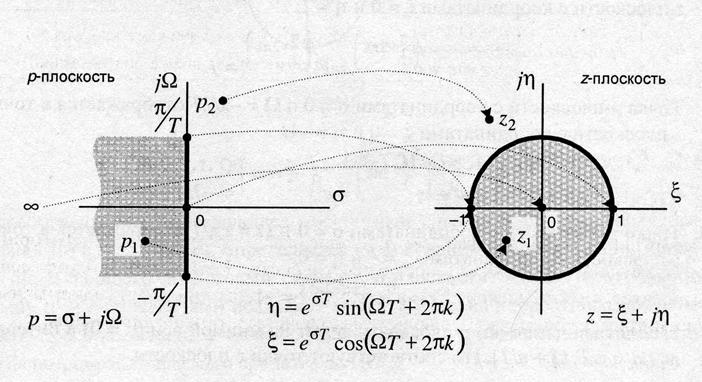
Рис. 3.1.
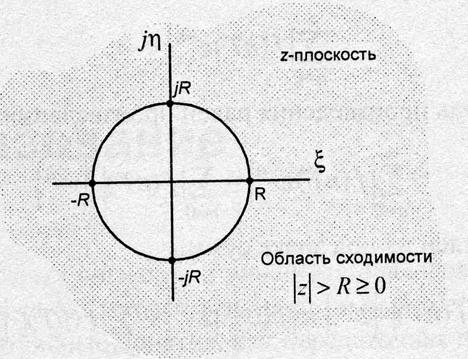
Соотношение между Z и P плоскостями (2).
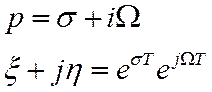
Откуда
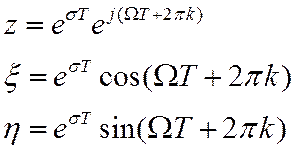
где ![]()
1. Мнимая ось плоскости Р переходит в бесконечное число окружностей единичного радиуса
![]()
2. ![]()
3. 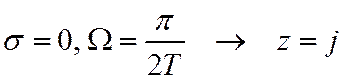
4. 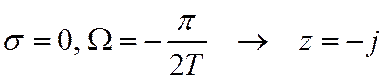
5. 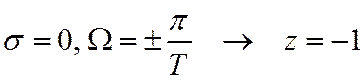
6. Т.о., прохождение точкой интервала 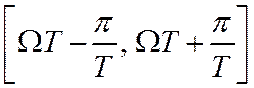 Точкам P-плоскости,
лежащим на мнимой оси
Точкам P-плоскости,
лежащим на мнимой оси ![]() соответствует прохождение
единичной окружности на Z-плоскости.
соответствует прохождение
единичной окружности на Z-плоскости.
7. Точки левой полуплоскости ![]() переходят
внутрь единичного круга
переходят
внутрь единичного круга 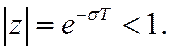
8. Точка ![]() соответствует центру
круга на Z-плоскости (Z=0).
соответствует центру
круга на Z-плоскости (Z=0).
9. Точки правой полуплоскости ![]() отображаются
во внешнюю область единичного круга
отображаются
во внешнюю область единичного круга
![]() .
.
Взаимно однозначное соответствие между P-
и Z-плоскостями можно установить только для полосы
между параллельными линиями, параллельными оси Y,
пересекающими ось X в точках ![]()
Рис. 3.2.
Свойства Z-преобразования.
1. Линейность.
Есть ЧП, равная сумме взвешенных ЧП
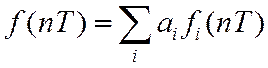
Для каждой их них
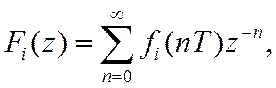
Тогда
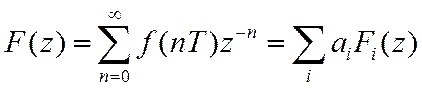
Доказательство:
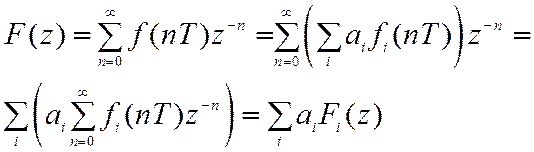
2. Теорема запаздывания.
Известно: ![]() .
.
Для задержанной последовательности ![]()
![]()
Доказательство:
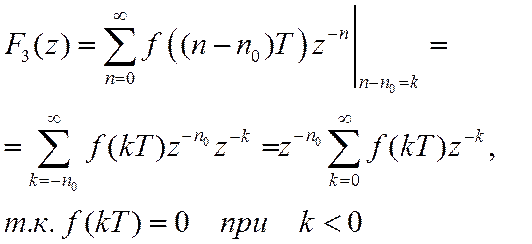
3. Z-преобразование свертки.
Свертке числовых последовательностей
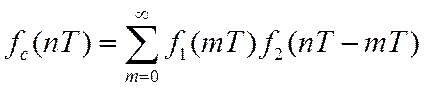
соответствует Z-изображение
![]()
Доказательство:
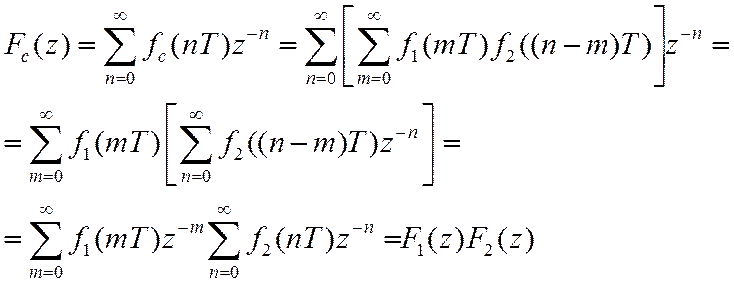
4. Z-преобразование числовой последовательности, умноженной экспоненту
![]()
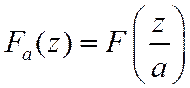
Доказательство:
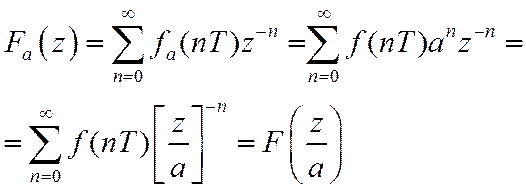
5. Дифференцирование.
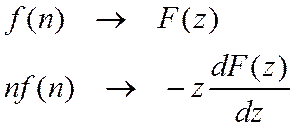
Доказательство:
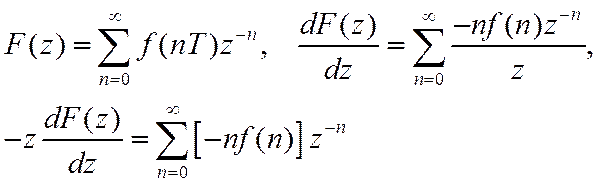
Z-преобразования типовых последовательностей (Т=1)
1. Единичный импульс
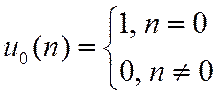
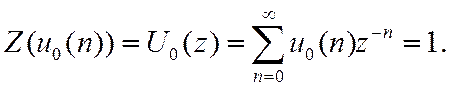
2. Задержанный единичный импульс
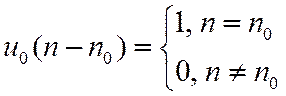
![]()
3. Единичный скачок
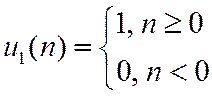
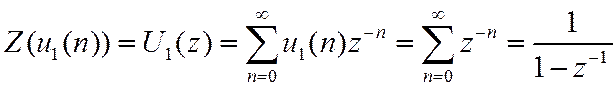
4. Дискретная экспонента.
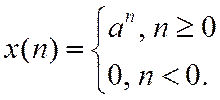
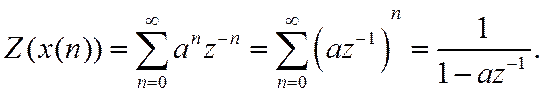
5. Числовая последовательность
![]()
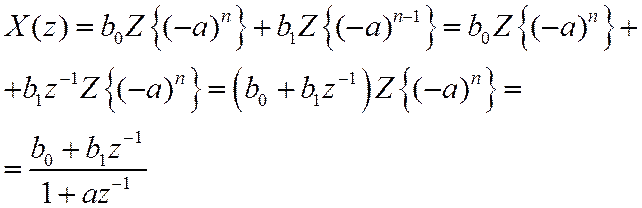
6. Доказать
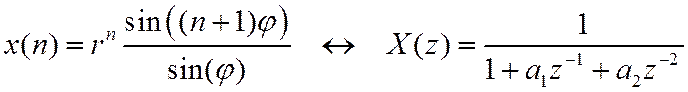
где
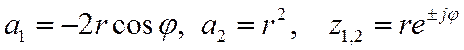
![]() - полюсы Z-образа.
- полюсы Z-образа.
Доказательство
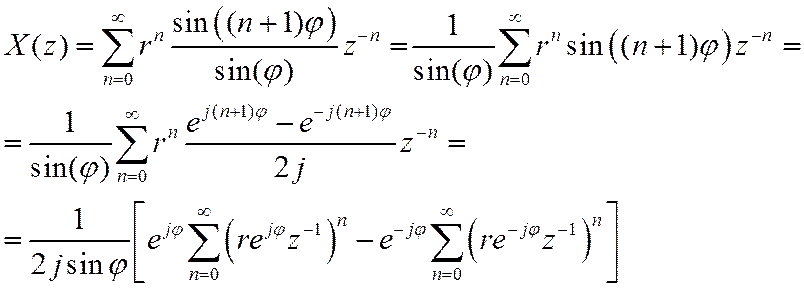
Учитывая
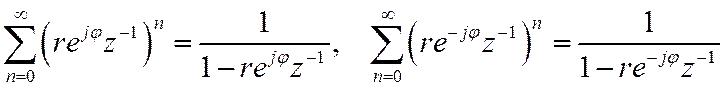
Запишем
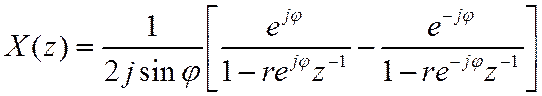
Т.о., полюсы ПФ располагаются в точках 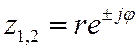 . Приведя выражение в скобках к общему
знаменателю и проведя сокращения, получим (25) с коэффициентами (24).
. Приведя выражение в скобках к общему
знаменателю и проведя сокращения, получим (25) с коэффициентами (24).
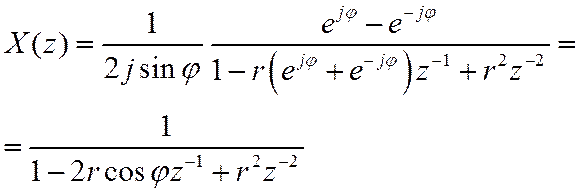
Таблица соответствий
Таб. 2.3.
Обратное Z-преобразование (A-214)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.