Z-преобразование. Свойства Z-преобразования. Z-преобразования типовых последовательностей. Обратное Z-преобразование, страница 2

Обратное Z-преобразования позволяет восстановить числовую последовательность по ее z-образу.

                                                                               

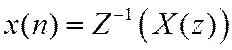
Было

                                                                                               

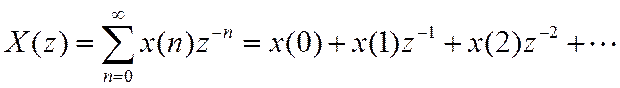
Т.о., значения последовательности  - это коэффициенты ряда при степенях .

Часто

                                                   

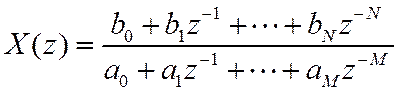
В этом случае соответствующую числовую последовательность можно найти одним из следующих способов

·  разложением в степенной ряд

·  использованием таблицы соответствий

·  разложением на элементарные дроби

·  вычислением контурных интегралов.

Метод разложения в степенной ряд

Для случая (28). Реализуется деление в столбик. Предварительно числитель и знаменатель (28) выражаются либо через уменьшающийся, либо через увеличивающийся показатель степени Z. Затем производится деление полиномов.

Пример.

Для

                                                 

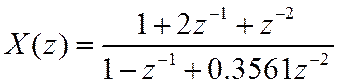
найти соответствующую числовую последовательность.

Выполним деление:

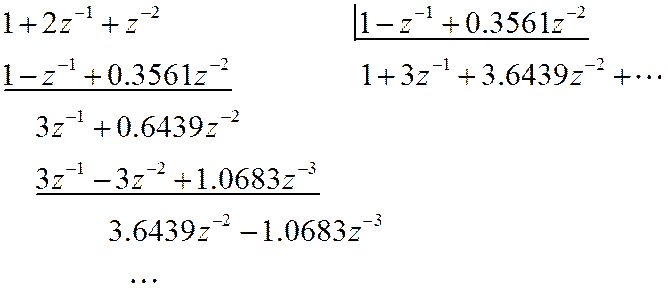
Следовательно,

                                                       

Перед делением можно исходное выражение преобразовать

                                                    

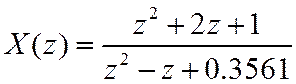
Метод деления в столбик можно реализовать так, что значения последовательности могут быть вычислены рекурсивно. Например, для

                                                                

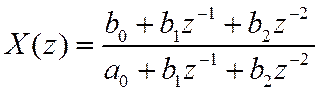
отсчеты исходной последовательности можно найти по алгоритму

                                                                                                

                                                                                                           

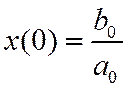
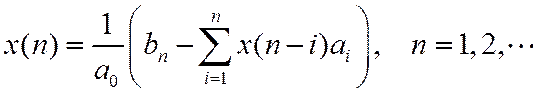
Использование таблицы соответствий.

Для заданного изображения непосредственно, или после некоторых преобразований, находят соответствующую числовую последовательность. Способ не отличается общностью.

Пример.

                                                           

                                                

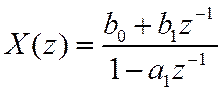
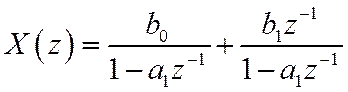
В силу линейности

                                                    

где

                                          

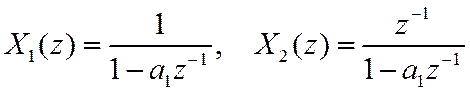
Из таблицы соответствий и с учетом теоремы запаздывания

Окончательно

                                                        

Разложение на элементарные дроби. (А-217)

                                                                           

Для

                                            

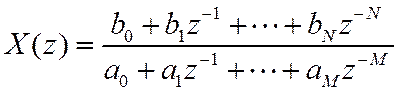
при можно разложить как

                                                                                                             

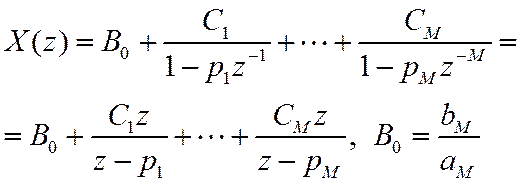
Коэффициенты  называют вычетами функции .

Если , то

Если , то дробь нужно сначала сократить.

Коэффициенты  можно найти следующим образом

                                                                   

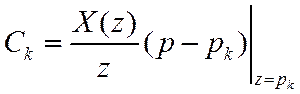
Для полюса m-го порядка в разложении на элементарные дроби должны входить слагаемые

                                                                                 

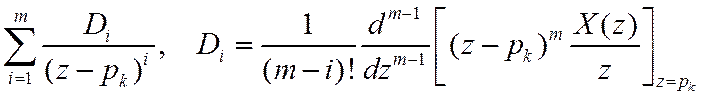
Пример.

Функция  содержит простые полюсы первого порядка. Найти обратное Z-преобразование.

                                                     

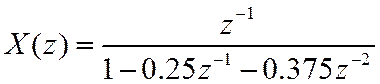
Умножим числитель и знаменатель на . И представим знаменатель в виде

                                                 

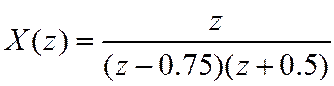
Т.к. N<M, то разложение на простейшие дроби будет иметь вид

                         

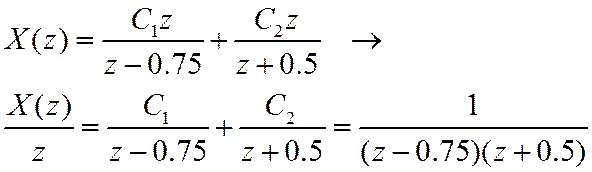
Определим константы

              

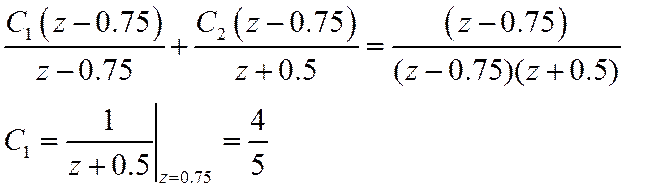
Аналогично .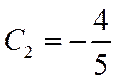

                                                

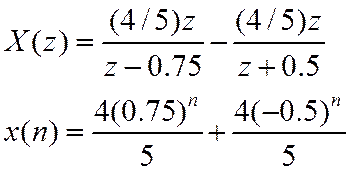
Пример.

Функция  содержит полюс второго порядка.

                                                    

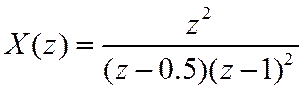
Разложение на элементарные дроби

                                           

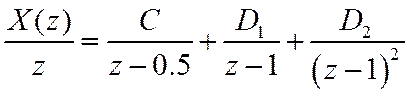
Константа С=2. Для определения D воспользуемся (37) при m=2, i=1,2.

       

                                    

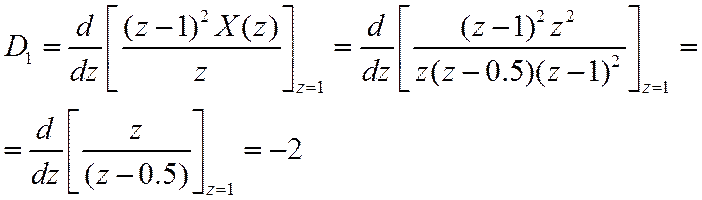
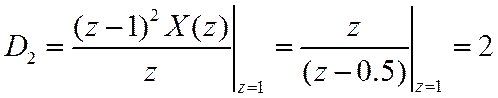
Выражение для

                                           

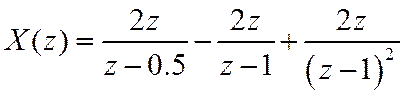
Из таблицы соответствий

                                                    

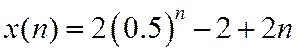
Метод вычисления контурных интегралов.

Вычисляется интеграл по контуру, охватывающему все полюсы функции

                                                               

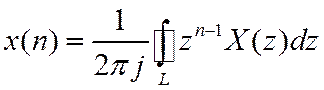
Интеграл определяется вычетам

и функции  в полюсах

                                                                                                         

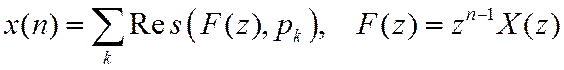
Для полюса порядка m вычет определяется

                                                                                           

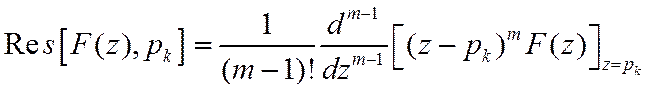
Для простого полюса

                                                                                                                

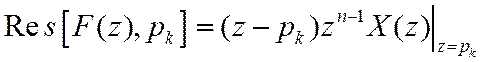
Пример.

Для

                                                    

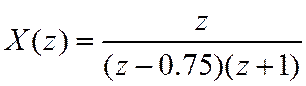
найти соответствующую числовую последовательность.

                                      

                                

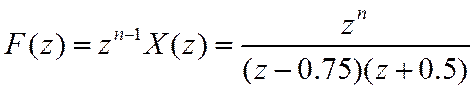
Т.к. полюсы простые, то

                                  

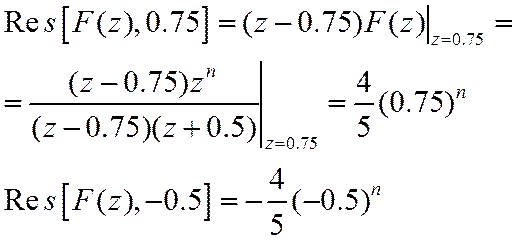
Окончательно

                                               

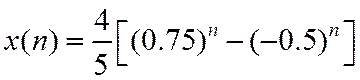
Задание.

Для

                                                    

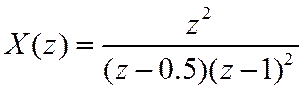
найти соответствующую числовую последовательность.

Сравнение различных способов вычисления числовой последовательности по Z-образу.