Осесимметрические задачи теории упругости. Состояние упругости. Закон Гука. Решение системы линейных уравнений с ленточной матрицей коэффициентов, страница 3

По замыслу дискретизации перемещения q_i  независимы и однозначно определяют положение системы, т.е. под величинами q_i  можно понимать обобщённые координаты. В этом случае P_j-обобщённая внешняя сила, являющаяся частью полной обобщенной силы, которая, как известно, для системы находящейся в равновесии, равна нулю.

Равенства (1), выражающие физический смысл линейной упругости, играют роль уравнений, как только ставится задача отыскания перемещений закреплённой системы по заданным  внешним силам. Именно такую форму записи имеют

разрешающие уравнения при конечномерных подходах к решениям типовых задач механики линейных упругих систем. На пути к этим решениям, очевидно,

необходимо изучить способы определения коэффициентов матрицы жёсткости

(2).Перейдём к  внутренней форме закона Гука. В одномерном процессе растяжения стержня напряжение s выражается через деформацию e:s=E*e Модуль упругости Е определяется, как производная , вычисленная при e=0. В случае, когда тензоры [T_s] и [T_e] имеют общий вид, закон Гука записывается в форме

s₁=c₁₁*e₁+c₁₂*e₂+…+c₁₆*e₆ ;

s₂=c₂₁*e₁+c₂₂*e₂+…+c₂₆*e₆ ;

                     ……………………………..                 (3)

s₆=c₆₁*e₁+c₆₂*e₂+…+c₆₆*e_{6 ,}

  или в символических обозначениях

                                                     {s}=[C]×{e}.            (4)

 В этих равенствах столбцы напряжений {s} и  деформаций  {e}  формируются из элементов тензоров [T_s]  и [T_e]   следующим образом:

{s}=

{e}=

Матрица

[C]=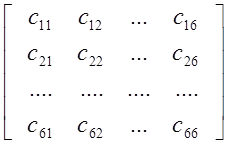

называется матрицей внутренней жёсткости или матрицей упругости. Полагая

все e_k=0 , кроме `e<sub>j</sub>=1 устанавливаем, что коэффициент c<sub>ij</sub>  численно равен напряжению s<sub>i</sub> в рассматриваемой точке, соответствующему деформации `e_j=1.     Понимая под коэффициентом с_ij  производную напряжения s_i  по деформации e_j , т.е.  c_ij=, можно этот коэффициент называть модулем упругости- константой материала, определяемой лишь экспериментально.      

   Список использованной литературы:

1. Сегерлинд Ларри Дж. Применение метода конечных элементов.-М.: Мир, 1979. -392 с.
2. Галлагер, Ричард, Метод конечных элементов. Основы, М.: Мир, 1984г.

ПРИВЕСТИ ВСЕ В ПОРЯДОК И ПОТИХОНЬКУ ПРОГРАММИРОВАТЬ ЭТОТ ПРИМЕР

Пример

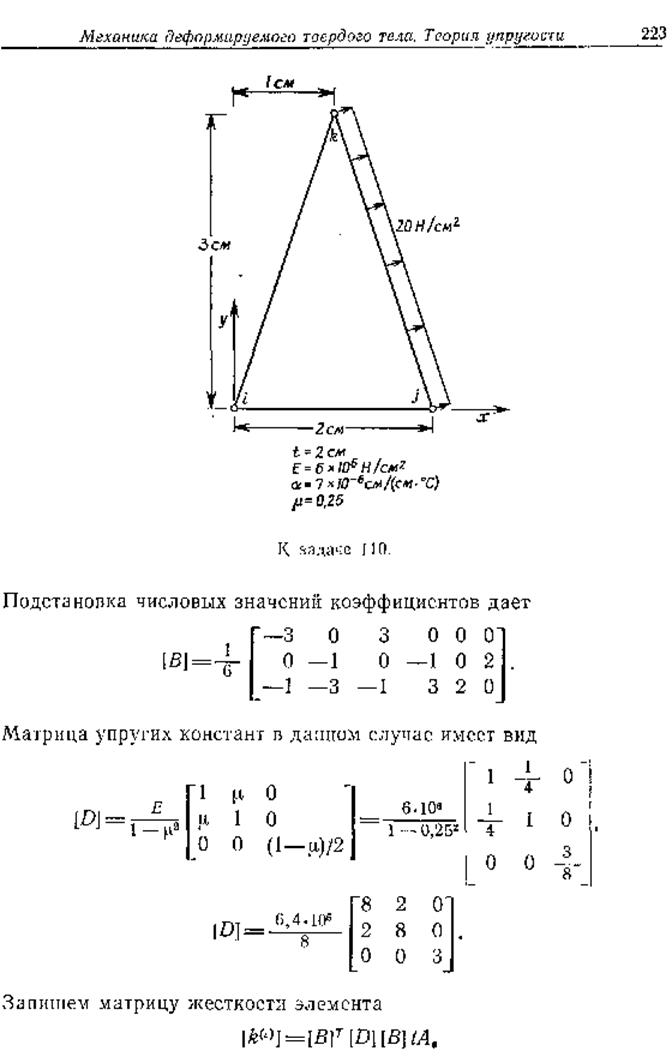
110. Нужно вывести определяющие элемент уравнения для изо­браженного ниже элемента в случае плоского напряженного со­стояния. Перпендикулярно к стороне jk действует равномерно распределенная нагрузка интенсивности 20 Н/см². Элемент испы­тывает также тепловое расширение вследствие повышения его тем­пературы на 15°.

Запишем матрицу градиентов

, Р' °

[5]-^ 0 с,

Ci Ь, где Л ==(3-2)/2=3 см²,

&,=У,-У,=-3,

b,=Y,-Y,=3,

^ci=^xk с,=Х.

 Механика деформируемого твердого тела. Теория упругости

1см

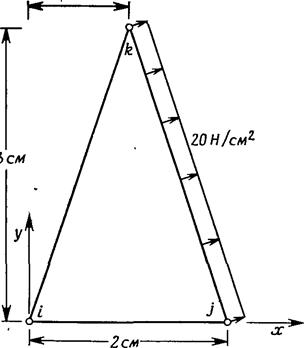
t'lCM

E=6l^Ю⁶^^/cм^г ol=7'^10~⁶c»l/(c»l•°C) у =0.25

К задаче 110.

Подстановка числовых значений коэффициентов дает

Г—3  0   3   0 0 01 [В]=-^-   0—1   0—102 ^—1 —3—1   320

Матрица упругих констант в данном случае имеет вид - ,  1

								" 1	1	0"
	"1	^	0						4
Е	р, 0	1 0	0(1-}х)/2		6.	10s	2	1	1 0	0 3 ~8'
l—(i2					1—	0,25		40
				'8	2	0'
		\D]=	6,4.106	2	8	0	,
			8
				0	0	3

[D]=

Запишем матрицу жесткости элемента

W=[B]T[D}[B]tA,

224           Глава 12

-—3		0 —1-
1В№1=-^	03 0	—1 —3 0 —1 —1 3			6,4.106	'8 2 0" 280,
					8
	0	0 2				003
	0	2 0
-—24					—6 —3'
			—2		—8 —9
[В]7 [С	)]=6	,4.10°	24 3		6 —3 —8 9
		48
			0		0 6
			4		16 0