Осесимметрические задачи теории упругости. Состояние упругости. Закон Гука. Решение системы линейных уравнений с ленточной матрицей коэффициентов, страница 2

Интеграл, включающий поверхностные нагрузки, вычисляется с помощью L-координат. Этот интеграл имеет вид

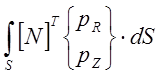
где   и -компоненты поверхностной нагрузки в направлениях r и z .Рассматривая сторону между узлами I  и J  ,вдоль которой    ,   будем иметь

 = 

 

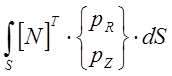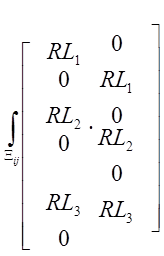
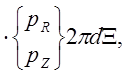
   После подстановки выражения (*):

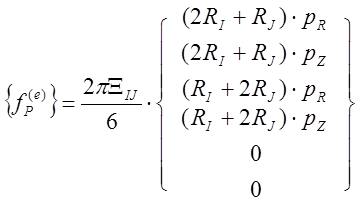
по-прежнему означает длину стороны между узлами I  и J. Последнее           соотношение обладает свойством, а именно оно применимо к поверхности ,ориентированной произвольным образом. Если рассматривать вертикальную поверхность, то R_I=R_J=R,

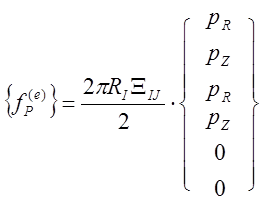
Эта формула показывает, что компоненты нагрузки поровну распределяются между узлами. Этот результат идентичен тому, который получен для двумерной задачи. С другой стороны, если рассматривается горизонтальная поверхность,, и тогда на наиболее удаленный от оси вращения узел будет приходиться большая часть нагрузки.

               Напряжения в элементах вычисляются по закону Гука:

 С учетом формулы  напряжения могут быть выражены через       узловые перемещения:

    

Записывая подробно это равенство, можно убедится ,что нормальные напряжения зависят от величины   ,которая является функцией r  и  z  ,так как от r  и z  зависят коэффициенты матрицы . Таким образом можно вычислить напряжения во многих различных точках внутри элемента. Компонента напряжения сдвига, однако, оказывается постоянной внутри каждого элемента.

Состояние упругости. Закон Гука

   Материал при деформировании обычно находится в промежуточных состояниях: упругопластических, вязкопластическом, вязкоупругом и др. Для построения механических моделей материалов эти состояния идеализируются и   лишь  после   выявления   специфических      особенностей  каждой идеализации делаются попытки построить модели, приближающиеся к реальным состояниям.        упругое, пластическое, вязкое состояния и состояние разрушения.

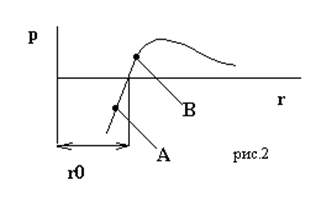Упругое состояние характеризуется отсутствием диссипации энергии. Упругодеформированное тело после снятия нагрузки полностью восстанавливает свою форму и объём. В процессах, в которых силы инерции ещё заметной роли не играют, упругая деформация cчитается мгновенной. В упругом состоянии межатомные расстояния изменяются, но атомы остаются в узлах решётки. Практически для любого материала, находящегося в упругом состоянии, существует диапазон деформирования, характеризующийся линейной связью между силами и перемещениями, напряжениями и деформациями. На схеме силового взаимодействия микрочастиц (рис.   1 ) - это линейный участок АВ.

Рассмотрим две формы закона Гука, отражающего указанную линейность связи. Во внешней форме выразим связь между силами и перемещениями дискретизированной линейно – упругой системы, во внутренней форме установим зависимость между напряжениями и деформациями. В простейшем cлучае  дискретизированной системы с одной степенью свободы закон Гука во внешней форме имеет вид k×q =P, где q –перемещение узловой точки под действием обобщённой внешней силы P. Коэффициент пропорциональности k называется коэффициентом жёсткости. Его размерность  зависит от размерности

величин P и q. Если P-сила,q – линейное перемещение, то размерность k –H/м.

Если P-пара сил, q-угловое перемещение, то размерность k –H м. Положив q= 1, oпределяем, что коэффициент жёсткости численно равен силе, создающей это перемещение. Для системы с n степенями свободы закон Гука приобретает вид

                                          k₁₁*q₁+k₁₂*q₂+_…+k_1n*q_n=P₁;

                                          k₂₁*q₁+k₂₂*q₂+…+k_2n*q_n=P₂;

                                          ………………………………

                                          k_n1*q₁+k_n2*q₂+…+k_nn*q_n=P_n,

или в символической системе [K] {q}={P}      (1)

  где {q}=-столбец перемещений;

        {P}=-столбец внешних сил;

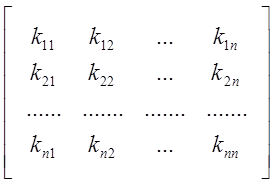                           [K]=               (2)                                                                                                                                 

-  матрица внешней жёсткости.

 Физический смысл коэффициента жёсткости k_ij выявим, наложив связи на    все  степени свободы, кроме  j-ой  , по которой дадим единичное перемещение                              `q_j=1.Все остальные перемещения q_k=0 (j¹k) . Тогда  k_ij=P_i , т.е коэффициент численно равен реакции в i-й  связи при условии, что по j-му направлению дано единичное перемещение.