ОСОБЕННОСТИ РАСЧЕТА НИЗКОЧАСТОТНОЙ
СТРУКТУРНОЙ СОСТАВЛЯЮЩЕЙ ТРАНСПОРТНЫХ СРЕДСТВ
Иванов Н.И., Санников В.А.
(Россия, Санкт-Петербург, Балтийский государственный технический
университет)
Анализ распределения уровней звукового давления и его интенсивности с целью снижения до нормируемых значений необходим прежде всего для компоненты структурного шума, являющейся следствием вибрации ограждающих исследуемый на шум полезный объем конструкций. При этом воздушная, высокочастотная составляющая шума достаточно хорошо поддается аналитическому и экспериментальному измерениям, а данная компонента всецело определяется уровнями низкочастотных вибраций (до 300 Гц), создавая значительные трудности в проектировании тонкостенных (а, следовательно, нежестких) конструкций транспортных средств. Уже из понимания этого ясно, что влияние на ее уровни определяются в первую очередь возможностью снижения вибрации протяженных элементов - панелей, а значит, методами строительной механики машин, динамической жесткостью их корпусных элементов. Несмотря на то, что коробчатые конструкции панелей, обладают спектром более высокой частоты, как более жесткие, они являются материалоёмкими и трудоёмкими по сравнению с одностенными, что и приводит к их удорожанию в массовых производствах. Поэтому разработка, освоение и внедрение предварительно напряженных (деформированных принудительно) панелей для повышения спектра их колебаний требует прогнозирования как величин деформирования, так и уровней ожидаемой шумности - вибрации, что и выполняется программным обеспечением - компьютерным моделированием физико-математических моделей. Вычислительный эксперимент, основанный на анализе физико-математической модели процесса, наполненный конкретикой по физическим и механическим свойствам конструкций, конфигурации воздушных объемов и основных излучающих звук панелей, характером и видами нагружения, граничными условиями, позволяет эффективно разрабатывать и планировать рекомендации по практическим мероприятиям снижения вибрации, шума, как на стадии проектирования, так и на этапах отработки изделий ТМ. В качестве основы расчетов предлагается метод конечномерных моделей [1], достаточно эффективно зарекомендовавший себя в различных областях техники. Однотипность решаемых вычислительных процедур обоснована единством подхода - описания математическими аналогами решаемых систем уравнений.
Широкодиапазонное обобщающее структурно-механическое уравнение описывающее волновые, колебательные и нестационарные динамические процессы в сплошных средах в общем случае может быть представлено в виде
ð(X i ,t)=f (X i ,t) , (1)
где ð -Д'аламбертиан, а f(X i ,t) -функция выполняющая роль нагрузки и, при необходимости, требуемых параметров среды [1].
Анализ поставленных задач выполняется применением высокоточных элементов конечномерного подхода, аппроксимацией во времени двух или трехслойными схемами решения основных уравнений:
динамического движения [M(t)]d2{Q(t)}/dt2 + [K(t)]{Q(t)} = {P(t)}, (1)
теплового баланса [C(t)]d{T(t)}/dt + [K(t)]{T(t)} + {F(t)}= {0}, (2)
или [C(t)]d{T}/dt
+ [K(t)]![]() 2{T}/
2{T}/![]() xi2
+{Q}V+{ai(T-T¥i)}Si + {qj(t)}S2={0}
, (2а)
xi2
+{Q}V+{ai(T-T¥i)}Si + {qj(t)}S2={0}
, (2а)
при {Tэл} наS3 , где: [C(t)], [K(t)]-матрица характеристик теплоемкости, теплопроводности; {Q}V–вектор столбец нагрузок вызванных: внутренними теплоисточниками в объеме V; {ai(T-T¥i)}Si –теплоотдачей на поверхности S1; {Q}S2 -теплопотокаминаS2; {Tэл}S3 –темпера-турой на S3, или в целом для общего вектора {F(t)}={Q}V+{ai(T-T¥i)}Si +{qj(t)}S2.
Решение уравнений (1) и (2) проводится методом Бубнова, индифферентного к наличию или отсутствию граничных условий, что соответствует их характеру, изменяемого во времени, для рассматриваемой конструкции
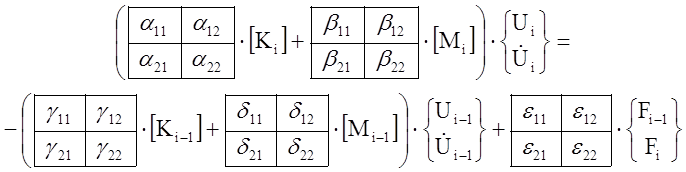 (1.а)
(1.а)
Здесь
векторы перемещений Ui-1искоростей
![]() в начальный момент
времени, при t=tн=0, равны соответствующим значениям U(0) и
в начальный момент
времени, при t=tн=0, равны соответствующим значениям U(0) и ![]() (0); {F(t)}
- текущий вектор нагрузки; i-
шаг итерации прямого решения, a a11, a12, b11, b12, g11 и т. д. - коэффициенты рекуррентного соотношения,
учитывающие координату времени на исследуемом отрезке D(ti);
[K]i, [M]i-1, Pi-1, Pi - матрицы и векторы параметров исследуемого объекта,
размерностью n´n
входящие в уравнение (1) на текущем и предыдущем шагах.
(0); {F(t)}
- текущий вектор нагрузки; i-
шаг итерации прямого решения, a a11, a12, b11, b12, g11 и т. д. - коэффициенты рекуррентного соотношения,
учитывающие координату времени на исследуемом отрезке D(ti);
[K]i, [M]i-1, Pi-1, Pi - матрицы и векторы параметров исследуемого объекта,
размерностью n´n
входящие в уравнение (1) на текущем и предыдущем шагах.
Выполняя интегрирование по координате времени t, D(ti) получаем рекуррентное соотношение двухслойной схемы расчетов нестационарного температурного поля
-(2×[K]i+![]() ×[C] i)×{Ui}=([K]i-1-
×[C] i)×{Ui}=([K]i-1-![]() ×[C] i-1)×{Ui-1}+ {Fi-1} + 2×{Fi}. (2а)
×[C] i-1)×{Ui-1}+ {Fi-1} + 2×{Fi}. (2а)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.