Диффузионные задачи и решения для элементов

28.2.  Д и ф ф у з и о н н ы е      з а д а ч и     и      р е ш е н и я    д л я    э л е м е н т о в

Первую задачу формулируем,  как это было в теме 20.2, для полуограниченного тела.

Дано полуограниченное  тело (рис. 25.2-644 б) при неизменной температуре Т из материала с относительной атомной концентрацией летучего элемента (начальная концентрация). В начальный момент времени материал  помещается в среду с относительным  парциальным давлением этого элемента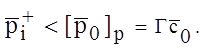. Испарение происходит при граничных условиях третьего рода. Требуется найти распределение концентрации (Y,t)  по глубине Y в произвольный момент времени t.

Общее решение представлено  уравнением (20.9) с соответствующими  заменами ко-  ординат, тепловых характеристик – диффузионными, q на J (как в задачах на охлаждение):

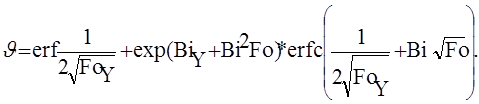                                               (3)

При интенсивном переносе, когда аргументы функций ехр и еrfc много больше   1,   второе слагаемое практически равно нулю, решение принимает вид

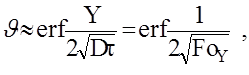                                                                                     (4)

 который  получают при граничных условиях первого рода, когда концентрация на поверх- ности удерживается на неизменном уровне: (0, t) = const. В данном случае при Y=0 правая часть равна нулю:

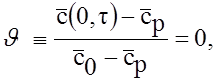
следовательно, на поверхности

           

т.е. здесь сразу же устанавливается и поддерживается равновесное значение

         

          В то же время на нижней границе обедненной зоны Y_* концентрация летучего компонента  еще близка  к начальному значению, и здесь

            

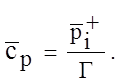
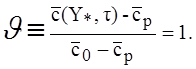
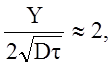Из рис.20.2-568 ясно, что в этом случае аргумент  так что глубина                                                                                                                (5)

Поскольку эти частные решения выводы обусловлены большим значением Biо, подобная ситуация складывается при сочетании весьма энергичного отвода летучих из пограничного слоя (высокое значение коэффициента массоотдачи  b) с очень вялой диффузией летучего элемента из глубины пластины к рабочей поверхности. Поверхность как бы сразу подчиняется диктату среды и быстро приходит в уготованное ей неизменное состояние.

Во второй задаче, как при теплообмене, будем иметь в виду неограниченную пластину конечной толщины и одинаковые условия испарения на обеих поверхностях. Повторяя рассуждения темы 22.1, записываем решение теплопроводности с таким же, в центральной плоскости,  положением начала координат, но другим, диффузионным, содержанием  критериев подобия  и левой части :

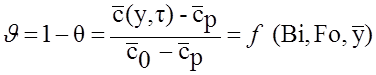.                                                             (6)

Значения функции J, как мы знаем по теории теплопроводности, представлено в виде номограмм 22.2-575, и нет нужды заниматься вычислениями по весьма сложным зависимостям. Тем не менее,  аналитическое решение полезно для выводов по предельным режимам испарения.

При  Bi < <1 (вялый  массообмен, быстрая диффузия или тонкая стенка) согласно 22.3                

         ехр(- Bi*Fo) * соs,                                                                      (7)

а если Bi < 0,1,   то  соs » 1,  решение не зависит от глубины у, т.е.  стенка обедняется  практически равномерно.

При Bi >>1(быстрый массообмен, вялая диффузия или толстая стенка) согласно 22.4

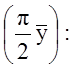1,27 ехр(- 2,47 Fo) соs                                                                     (8)

          в центре ( =  0)

         = 1,27 ехр(- 2,47 Fo),                                                                                      (9)

и уже при Fo = 2   J_ц » 0, с_ц º с(0, t) » с_р, стенка обедняется  по всему сечению практически до равновесной со средой концентрации;

           на поверхности ( = 1)

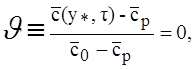                     `с(`у,t) º`с(1,t)=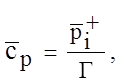

т.е. концентрация с cтремительно опускается до предельного равновесного  уровня и впредь сохраняется (род граничных  условий меняется с третьего на первый). При таких обстоятельствах и условии типа (20.6)

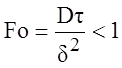                                                                                                            (10)

концентрационное поле можно рассчитывать, как в полуограниченном теле. С  учетом  нового положения  начала координат - не на рабочей поверхности, а в центре пластины:

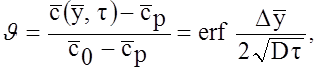                                                                            (11)

где заглубление Dу = d - у, D= 1 -.