Диффузионные задачи и решения для элементов, страница 2

Все решения распространяются на  противоположный испарению процесс поглощения   (рис. 25.2-644 а) - в  этом случае

q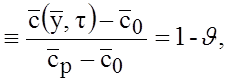

и на стенки с односторонним испарением  - в этом случае в качестве размера d принимают толщину стенки (а не половину толщины, как при двухстороннем процессе).

28.3. Д и ф ф у з и о н н ы е    р е ш е н и я    д л я    д в у х а т о м н ы х    г а з о в

При дегазации  или  растворении,  в отличие от испарения,  концентрация и парциальное давление  связаны  друг с другом  степенными  уравнениями (26.1) 

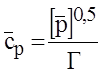`или                                                                          (12)

и в качестве для граничного  условия третьего рода  вместо (1) имеем

,

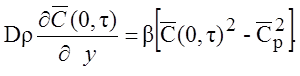где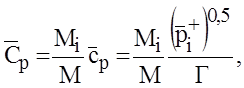

M_i, М – молекулярная масса активного компонента и материала соответственно.                                                                  

Сравните с тем, что было в теории теплопроводности. Налицо принципиальное отличие - нелинейность, аналитическое решение уравнения диффузии не просто осложняется, оно становится невозможным, и остается уповать на численные методы. Тем не менее, простой прием позволяет для  быстрой ориентировки использовать предыдущие выводы: представляем разность квадратов  в правой части уравнения как произведение разности и суммы, замораживаем сумму на одном из предельных уровней:

максимальном

                                                                                     (13)

или  минимальном   (меньшем из двух значений:   или )

                                                                                        (14)

получаем        

,                                                                       

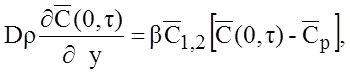где  имеет одно из граничных значений -`   или `,

а затем действуем, как при переносе элементов, но с условным коэффициентом переноса

                                                                                                            (15)

При изменившемся содержании β и  все предыдущие диффузионные решения для элементов остаются в силе для двухатомных газов.

             28.4. О б о б щ е н и е  (для избирательного массопереноса )

             Для превращений по типу    [S] «  S (избирательное  испарение),

             [S]    « 0,5 S₂ (дегазация ),     S₂ « 2 [S] (растворение)

скорость, параметр переноса, степень неравновесности, отклонение от равновесного давления определяются зависимостями из обобщений 15.2, 16.4 аналогичными при m = 1 (если принимать для дегазации и растворения скорость переноса не в атомарном, а в молярном представлении). Единственное и принципиальное отличие заключается в том, что равновесные давления рассчитывают через константу Генри Г и молярную концентрацию с. При вычислении  характеристик переноса рекомендуется использовать табл. 1- 601 со следующим  содержанием параметров:

[`р]_р- равновесное давление активного компонента над материалом, 

` – относительное парциальное давление этого компонента в среде,

  Г –   константа  Генри (γ`р_р -для испарения,  γ К_р  -для дегазации и растворения),

  g  –   коэффициент активности растворенного элемента  в материале,

  `с₀-   атомная  доля этого элемента в материале исходного состава (не выше предела растворимости !) ,

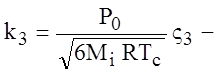    константа скорости газовых стадий ( обратной при испарении и  дегазации, прямой - при растворении),

   М _i- атомная (при испарении) или молекулярная (при дегазации и растворении) масса активного компонента.

                                                                                                            Таблица 1-601

  Характеристики  избирательных процессов

Процесс	Определяющее соотношение	Молярная скорость rv  в предельных режимах
		Равновесный     (Jc << 1)	Кинетический     (Jc >> 1)
Испарение
Дегазация
Растворение

Решения по нестационарной диффузии для элементов  (тема 28.2) распростра няются  на двухатомные газы при новом содержании параметров:

         ,

где условная массовая доля активного элемента в материале  оценивается  по  начальному и  равновесному  значениям на предельных уровнях:

максимальном

,

или  минимальном (меньшем из двух значений или )

.