Расчет плоских стержневых систем методом конечных элементов

БАЛТИЙСКИЙ  ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ

«ВОЕНМЕХ» имени Д.Ф. Устинова

────────────────────────────────────

КАФЕДРА МЕХАНИКИ ДЕФОРМИРУЕМОГО

 ТВЕРДОГО ТЕЛА

КУРСОВОЙ ПРОЕКТ

Тема: «Расчет плоских стержневых систем

методом конечных элеметов»

Преподаватель:         Высоцкий В.И.

Студент:         Бертова А.В.

Группа:      К-301

Санкт-Петербург

2004г.

1.  Формулировка задания

Требуется:

Ø  для заданной стержневой системы определить прочные размеры поперечных сечений;

Ø  оценить максимальное напряжение в системе, если на нее воздействует температурный перепад в 100 град. (прежняя нагрузка отсутствует).

Дано:

Е=2·10⁶ (кГ/см²);

μ=0,3;

[σ]=1600 (кГ/см²);

а=100 (см);

q=1 (кГ/см);

ΔТ=100°С.

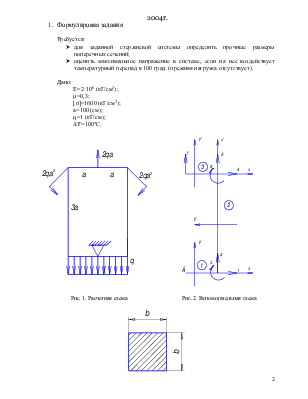
Рис. 1. Расчетная схема	Рис. 2. Вспомогательная схема

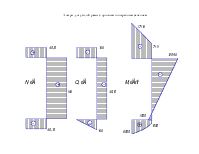
Рис. 3. Профиль используемых в конструкции стержней

2.  Результаты полученные после запуска процедуры вычислений для первой итерации

 C        ЗАДАНИЕ 1 (1-ая итерация)

                    ИСХОДНЫЕ ДАННЫЕ

   7  3  5

    .1000E+01   .1000E+01   .1000E+01

    .1000E+01   .1000E+01   .1000E+01

    .1000E+01   .1000E+01   .1000E+01

    .1000E+03   .3000E+03   .1000E+03

    .1000E+01   .0000E+00   .0000E+00

   МАТРИЦА ИНДЕКСОВ

   0  0  0  1  2  3

   1  2  3  4  5  6

   0  7  0  4  5  6

              МАТРИЦА НАПРАВЛЯЮЩИХ УГЛОВ

    .0000E+00   .9000E+02   .9000E+02   .0000E+00

    .9000E+02   .0000E+00   .1800E+03   .9000E+02

    .0000E+00   .9000E+02   .9000E+02   .0000E+00

ВЕКТОР НАГРУЗКИ

    .0000E+00  -.5000E+02  -.8333E+03   .0000E+00   .0000E+00   .2000E+05   .1000E+03

РЕЗУЛЬТАТ

ГЛОБАЛЬНАЯ МАТРИЦА ЖЕСТКОСТИ

    .1000E-01   .1624E-09   .6667E-04  -.4444E-06  -.4055E-10   .6667E-04   .3345E-02   .6000E-03  -.4055E-10  -.3333E-02

   -.8112E-12   .0000E+00   .5333E-01  -.6667E-04   .8112E-12   .6667E-02   .0000E+00   .1000E-01   .1624E-09  -.6667E-04

   -.1218E-09   .3345E-02   .6000E-03  -.1200E-04   .5333E-01  -.6000E-03   .1200E-04

ИСКОМЫЕ ПЕРЕМЕЩЕНИЯ

     ПАРАМЕТР ОШИБКИ=  0

   -.4815E+04   .2861E+08  -.4889E+06   .4816E+04   .2864E+08   .1211E+07   .9753E+08

УЗЛОВЫЕ ОБОБЩЕН. СИЛЫ И УСИЛИЯ В ЛОКАЛЬНЫХ СИСТЕМАХ КООРДИНАТ

УЗЛОВЫЕ ОБОБЩ. СИЛЫ И УСИЛИЯ В 1-М КЭ

        P1          P2          P3          P4          P5          P6

    .4815E+02   .1852E-02   .6555E+04  -.4815E+02   .1000E+03  -.1555E+04

        N1          Q1          M1          N2          Q2          M2

   -.4815E+02   .1852E-02   .6555E+04  -.4815E+02  -.1000E+03   .1555E+04

                         УЗЛОВЫЕ ОБОБЩ. СИЛЫ И УСИЛИЯ В 2-М КЭ

        P1          P2          P3          P4          P5          P6

   -.1000E+03  -.4815E+02   .1555E+04   .1000E+03   .4815E+02   .1289E+05

        N1          Q1          M1          N2          Q2          M2

    .1000E+03  -.4815E+02   .1555E+04   .1000E+03  -.4815E+02  -.1289E+05

                         УЗЛОВЫЕ ОБОБЩ. СИЛЫ И УСИЛИЯ В 3-М КЭ

        P1          P2          P3          P4          P5          P6

   -.4815E+02   .1000E+03  -.1711E+05   .4815E+02  -.1000E+03   .7111E+04

        N1          Q1          M1          N2          Q2          M2

    .4815E+02   .1000E+03  -.1711E+05   .4815E+02   .1000E+03  -.7111E+04

3.  Вычисление прочных размеров сечения

По изгибающему моменту опасным сечением является сечение третьего стержня, в первом узле.

Из условия прочности определяем размер b:

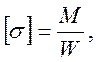
Осевой момент сопротивления:

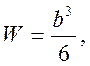
Искомый размер профиля:

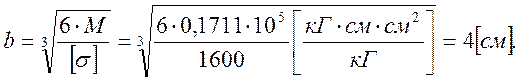
Используя принятый размер b, рассчитаем площади и осевые моменты инерции сечений:

;

.

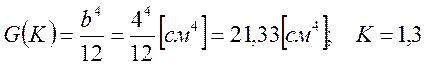4.  Результаты полученные после запуска процедуры вычислений для совершения второй итерации

C        ЗАДАНИЕ 1 (2-ая итерация)

                    ИСХОДНЫЕ ДАННЫЕ

   7  3  5

    .2000E+07   .2000E+07   .2000E+07

    .1600E+02   .1600E+02   .1600E+02

    .2133E+02   .2133E+02   .2133E+02

    .1000E+03   .3000E+03   .1000E+03

    .1000E+01   .0000E+00   .0000E+00

   МАТРИЦА ИНДЕКСОВ

   0  0  0  1  2  3

   1  2  3  4  5  6

   0  7  0  4  5  6

              МАТРИЦА НАПРАВЛЯЮЩИХ УГЛОВ

    .0000E+00   .9000E+02   .9000E+02   .0000E+00

    .9000E+02   .0000E+00   .1800E+03   .9000E+02

    .0000E+00   .9000E+02   .9000E+02   .0000E+00

ВЕКТОР НАГРУЗКИ

    .0000E+00  -.5000E+02  -.8333E+03   .0000E+00   .0000E+00   .2000E+05   .1000E+03

РЕЗУЛЬТАТ

ГЛОБАЛЬНАЯ МАТРИЦА ЖЕСТКОСТИ

    .3200E+06   .5198E-02   .2844E+04  -.1896E+02  -.1298E-02   .2844E+04   .1072E+06   .2560E+05  -.1298E-02  -.1067E+06

   -.3461E-04   .0000E+00   .2275E+07  -.2844E+04   .3461E-04   .2844E+06   .0000E+00   .3200E+06   .5198E-02  -.2844E+04