-.3900E-02 .1072E+06 .2560E+05 -.5119E+03 .2275E+07 -.2560E+05 .5119E+03
ИСКОМЫЕ ПЕРЕМЕЩЕНИЯ
ПАРАМЕТР ОШИБКИ= 0
-.1505E-03 .6706E+00 -.1146E-01 .1505E-03 .6716E+00 .2839E-01 .2286E+01
УЗЛОВЫЕ ОБОБЩЕН. СИЛЫ И УСИЛИЯ В ЛОКАЛЬНЫХ СИСТЕМАХ КООРДИНАТ
УЗЛОВЫЕ ОБОБЩ. СИЛЫ И УСИЛИЯ В 1-М КЭ
P1 P2 P3 P4 P5 P6
.4815E+02 .3678E-02 .6555E+04 -.4815E+02 .1000E+03 -.1555E+04
N1 Q1 M1 N2 Q2 M2
-.4815E+02 .3678E-02 .6555E+04 -.4815E+02 -.1000E+03 .1555E+04
УЗЛОВЫЕ ОБОБЩ. СИЛЫ И УСИЛИЯ В 2-М КЭ
P1 P2 P3 P4 P5 P6
-.1000E+03 -.4815E+02 .1555E+04 .1000E+03 .4815E+02 .1289E+05
N1 Q1 M1 N2 Q2 M2
.1000E+03 -.4815E+02 .1555E+04 .1000E+03 -.4815E+02 -.1289E+05
УЗЛОВЫЕ ОБОБЩ. СИЛЫ И УСИЛИЯ В 3-М КЭ
P1 P2 P3 P4 P5 P6
-.4815E+02 .1000E+03 -.1711E+05 .4815E+02 -.1000E+03 .7111E+04
N1 Q1 M1 N2 Q2 M2
.4815E+02 .1000E+03 -.1711E+05 .4815E+02 .1000E+03 -.7111E+04
5. Определение максимального напряжения
В опасном сечении продольное усилие и изгибающий момент имеют величины:
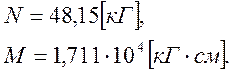
Следовательно:
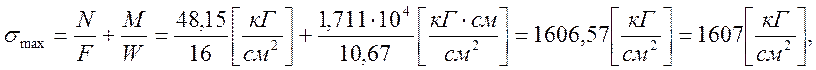
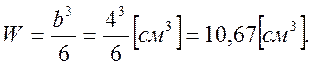
Перенапряжение:
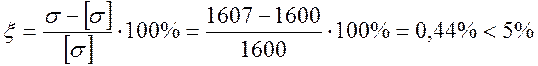 .
.
6. Проверка решения задачи с помощью условий статики
По локальным векторам Р выявим реакции в закреплениях:
В качестве условий равновесия выбираем уравнения:
а)
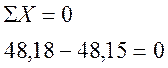
б)
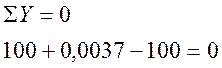
в)
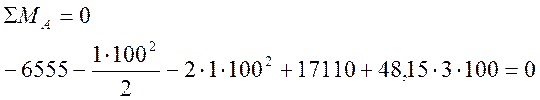
Все выражения практически вырождаются в тождества (0=0), что говорит о верности выполненного решения.
7. Запуск процедуры для вычисления узловых усилий при действии температурных перепадов
C ¦L-L=L+ 1(ЄхьяхЁрЄєЁэр чрфрўр)
ИСХОДНЫЕ ДАННЫЕ
7 3 5
.2000E+07 .2000E+07 .2000E+07
.1600E+02 .1600E+02 .1600E+02
.2133E+02 .2133E+02 .2133E+02
.1000E+03 .3000E+03 .1000E+03
.1000E+03 .1000E+03 .1000E+03
.1000E-04 .1000E-04 .1000E-04
МАТРИЦА ИНДЕКСОВ
0 0 0 1 2 3
1 2 3 4 5 6
0 7 0 4 5 6
МАТРИЦА НАПРАВЛЯЮЩИХ УГЛОВ
.0000E+00 .9000E+02 .9000E+02 .0000E+00
.9000E+02 .0000E+00 .1800E+03 .9000E+02
.0000E+00 .9000E+02 .9000E+02 .0000E+00
ВЕКТОР НАГРУЗКИ
.3200E+05 -.3200E+05 .0000E+00 .3200E+05 .3200E+05 .0000E+00 .0000E+00
РЕЗУЛЬТАТ
ГЛОБАЛЬНАЯ МАТРИЦА ЖЕСТКОСТИ
.3200E+06 .5198E-02 .2844E+04 -.1896E+02 -.1298E-02 .2844E+04 .1072E+06 .2560E+05 -.1298E-02 -.1067E+06
-.3461E-04 .0000E+00 .2275E+07 -.2844E+04 .3461E-04 .2844E+06 .0000E+00 .3200E+06 .5198E-02 -.2844E+04
-.3900E-02 .1072E+06 .2560E+05 -.5119E+03 .2275E+07 -.2560E+05 .5119E+03
ИСКОМЫЕ ПЕРЕМЕЩЕНИЯ
ПАРАМЕТР ОШИБКИ= 0
.1000E+00 -.9825E-05 .1121E-06 .1000E+00 .3000E+00 -.1311E-07 .3000E+00
УЗЛОВЫЕ СИЛЫ И УСИЛИЯ В 1-М КОНЕЧНОМ ЭЛЕМЕНТЕ
P1 P2 P3 P4 P5 P6
-.2980E-03 .2159E-02 -.1558E+00 .2980E-03 -.2159E-02 -.6012E-01
N1 Q1 M1 N2 Q2 M2
.2980E-03 .2159E-02 -.1558E+00 .2980E-03 .2159E-02 .6012E-01
УЗЛОВЫЕ СИЛЫ И УСИЛИЯ В 2-М КОНЕЧНОМ ЭЛЕМЕНТЕ
P1 P2 P3 P4 P5 P6
-.2284E-02 -.2814E-03 .6002E-01 .2284E-02 .2814E-03 .2441E-01
N1 Q1 M1 N2 Q2 M2
.2284E-02 -.2814E-03 .6002E-01 .2284E-02 -.2814E-03 -.2441E-01
УЗЛОВЫЕ СИЛЫ И УСИЛИЯ В 3-М КОНЕЧНОМ ЭЛЕМЕНТЕ
P1 P2 P3 P4 P5 P6
-.1514E-02 .3813E-03 -.1347E-01 .1514E-02 -.3813E-03 -.2466E-01
N1 Q1 M1 N2 Q2 M2
.1514E-02 .3813E-03 -.1347E-01 .1514E-02 .3813E-03 .2466E-01
8. Определение максимального напряжения
В опасном сечении продольное усилие и изгибающий момент имеют величины:
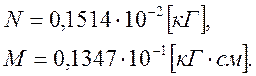
Следовательно:
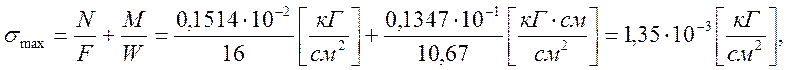
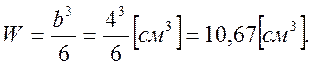
9. Проверка решения задачи с помощью условий статики
По локальным векторам Р выявим реакции в закреплениях:
В качестве условий равновесия выбираем уравнения:
a.
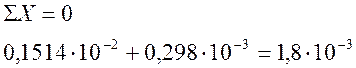
б)
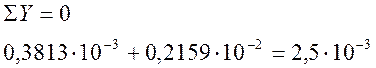
в)
Условия статики выполняются приближенно с удовлетворительными невязками.
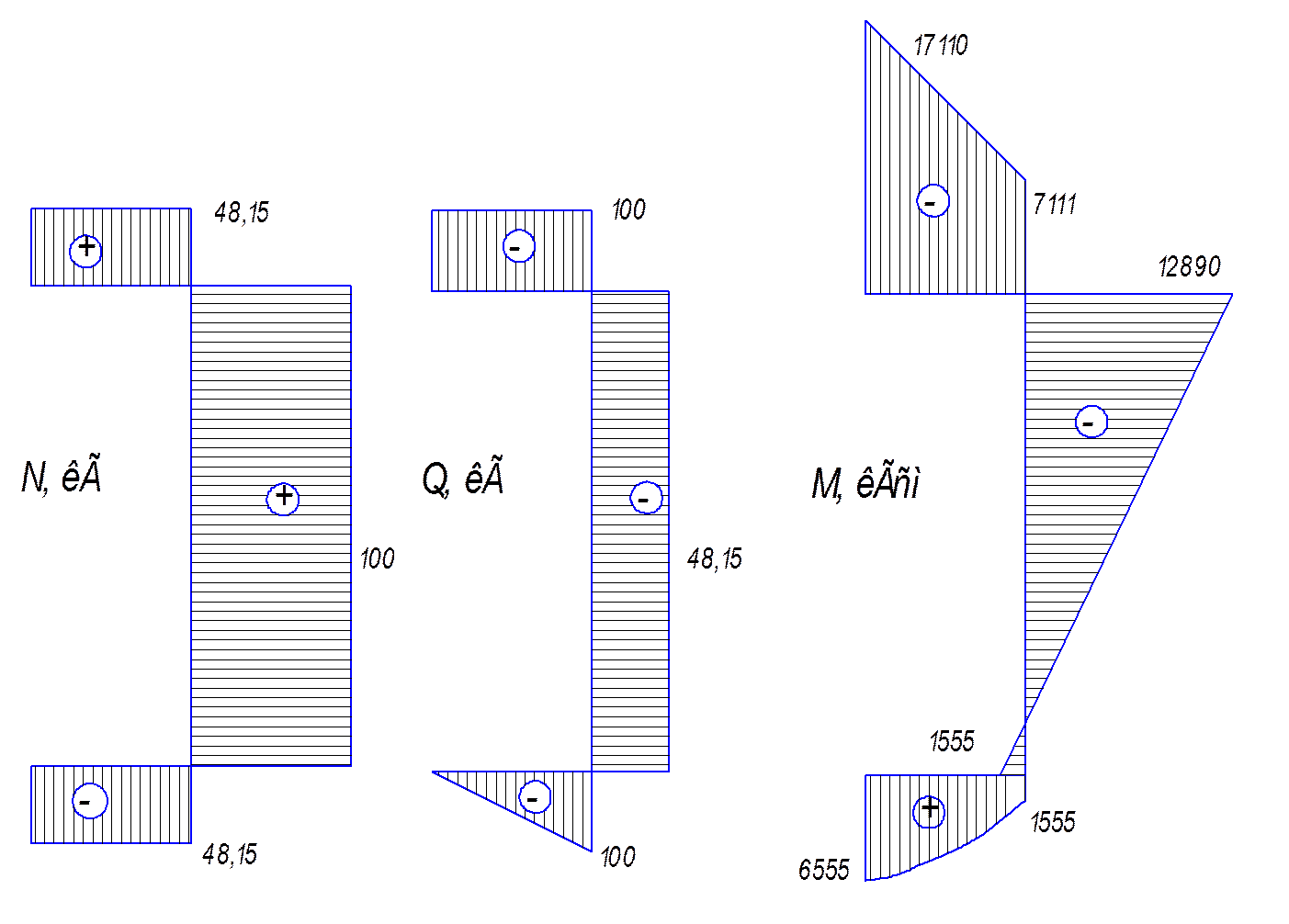
Эпюры для усилий рамы с прочным поперечным сечением
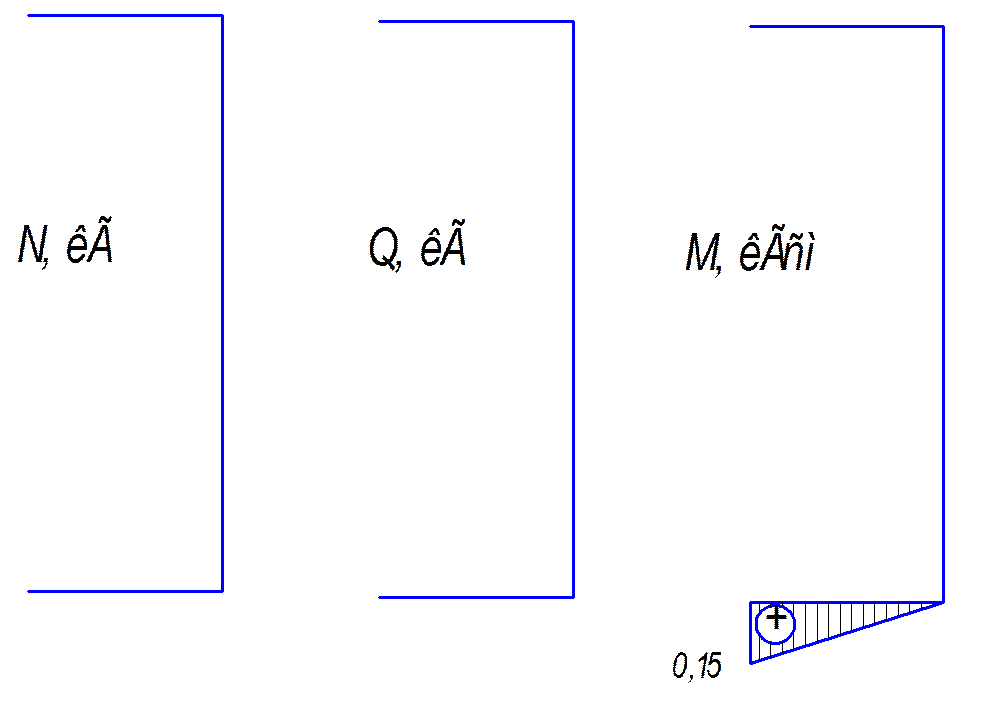
Эпюры для усилий рамы при перепаде температуры ΔТ=100°С
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.