Длительная усталость. Закономерности накопления усталостных повреждений. Способы повышения сопротивления усталости конструкций

ДЛИТЕЛЬНАЯ УСТАЛОСТЬ

1.  Закономерности накопления усталостных повреждений

Для проведения расчетов на циклическую долговечность при переменных нагрузках, помимо характеристик сопротивления усталости материалов, представленных в виде кривых и поверхностей усталости, необходима также информация о закономерностях накопления усталостных повреждений по мере увеличения числа циклов нагружения. Считается, что мера усталостного повреждения v равна нулю для начального состояния материала и равна единице для момента появления заметной усталостной трещины. Ее появление означает, что процесс разрушения переходит из стадии накопления собственно усталостных повреждений (из инкубационной стадии) в стадию роста усталостной трещины. Задача заключается в получении зависимости v = v (tr, п), где а — уровень амплитуд напряжений, устанавливаемый при испытаниях постоянным; п — число циклов нагружения (рис. 2.1). Когдаэта зависимость в координатах [v, n/N(о)], где N (о) — число циклов до разрушения при уровне напряжений а, описывается одним и тем же уравнением и не зависит явно от уровня напряжений а, процесс накопления усталостных повреждений называется автомодельным 141. Такой процесс показан на рис. 2.2. Так, в случае степенного закона накопления усталостных повреждений

(2.1)

v =

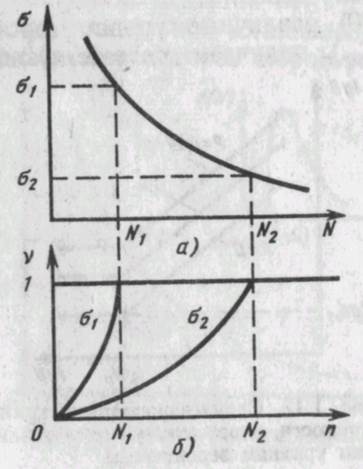
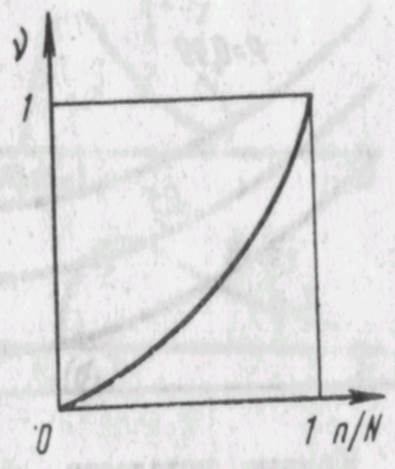
Рис. 2.1. Кривая усталости (а) и процессы накопления повреждений (б) при различных уровнях амплитуд напряжений ' / п/Н

п Рис. 2.2. Автомодельный процесс накопления усталостных повреждений при параметре ц const процесс накопления повреждении будет автомодельным, а при параметре ц, зависящем от уровня напряжений ц \\ (о), он не будет обладать этим свойством. При ц I получаем линейный закон накопления усталостных повреждений:

n/N.

(2.2)

          Для проведения расчетов

Для проведения расчетов Циклической долговечности при переменных нагрузках закономерности накопления усталостных повреждений удобно представлять в виде кинетических уравнений, связывающих скорости накопления усталостных повреждений от уже накопленного к данному моменту времени усталостного повреждения и от уровня амплитуд напряжений:

^-==/(v, а), (2.3)

где а — а (п) — процесс изменения амплитуд напряжений; п — число циклов нагружения.

Интегрируя уравнение (2.3) по v от 0 до 1 и по п от 0 до М„, определим искомую долговечность Л^, измеренную в числах циклов нагружения.

Простой результат получается в том случае, когда правая часть уравнения (2.3) может быть представлена в виде произведения двух функций, одна из которых зависит только от усталостного повреждения v, а другая — только от уровня напряжений сг:

v = /, (v) /₂ (а), (2.4)

где v — производная по числу циклов нагружения. В этом случае условие разрушения принимает следующий вид:

f*(o(n)]dn.

(2.5)

Поскольку при a - const долговечность N* -- N (о), а функция /₂ (о) — 1/N (а), то из соотношения (2.5) следует, что функция A (v) должна быть нормирована таким образом, чтобы интегралы в соотношении (2.5) были равны единице. При этом условие разрушения (2.5) принимает вид

(2.6)

В случае многоступенчатого режима нагружения (рис. 2.3) условие разрушения будет следующим:

16

Гусе» А. С.

(2.7)

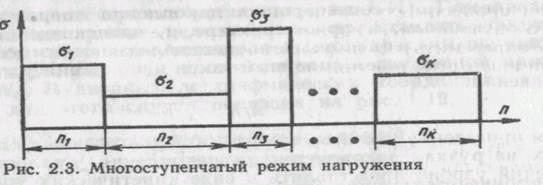
Рис. 2.3. Многоступенчатый режим нагружения

где /tj — число циклов нагружения на уровне напряжений о_;; ni— предельное число циклов нагружения до разрушения при уровне напряжений а\\ k— число ступеней процесса нагружения.

При нелинейном законе накопления усталостных повреждений величина 1/Nуже не является непосредственно мерой усталостного повреждения за один цикл нагружения, и соотношения (2.6) и (2.7) имеют в этом случае смысл правила линейного суммирования относительных долговечностей. Из соотношений (2.4) и (2.5) также следует, что для рассматриваемого случая условие автомодельности процесса накопления усталостных повреждений также выполняется. Таким образом, для нелинейных законов накопления усталостных повреждений, обладающих свойством автомодельности, так же как и для линейного закона накопления усталостных повреждений, справедливо правило линейного суммирования относительных долговечностей.

В случае степенного закона накопления усталостных повреждений (2.1) кинетическое уравнение разрушения имеет вид

ж-1^- (^

Разделив переменные в дифференциальном уравнении (2.3), получим

-i-v^''dv = d(v^) = -^. (2.9)

После интегрирования уравнения (2.9) для первого этапа нагружения имеем

*-№Г- ^(2ЛО)

где |н = ц Ю; n! = N (а_г).

Если процесс нагружения состоит только из одного первого этапа нагружения, то из условия v_x = 1 получаем постоянное значение долговечности n_x = niпри любом значении параметра ц₁₍ т. е. параметр нелинейности ц_х не влияет на условие разрушения при постоянном уровне амплитуд воздействий.

18