Длительная усталость. Закономерности накопления усталостных повреждений. Способы повышения сопротивления усталости конструкций, страница 3

Р = Щ/|*1 == 1/«. (2-19)

Экспериментальное определение зависимостей (2.18) и (2.19) может быть выполнено при двухуровневых испытаниях, проводимых, например, по схеме, показанной на рис. 2.4, в. В этом случае из условия разрушения (2.13)

(2.20)

Пока не имеется достаточных экспериментальных данных о действительных значениях функций а, которые можно было бы использовать на практике. Поэтому экспериментальное определение этой функции остается актуальной задачей при исследовании усталостной долговечности конструкций.

Помимо расчетов на долговечность, истинные закономерности накопления усталостных повреждений по мере нагружения могут быть эффективно использованы еще и при разработке методик ускоренных ресурсных испытаний конструкций и построении для них кривых и поверхностей усталости. Пусть, например, требуется оценить число циклов до разрушения Л^ на уровне напряжений ol когда этот уровень относительно низок, а число niнастолько велико (рис. 2.6, а), что довести испытание на этом б

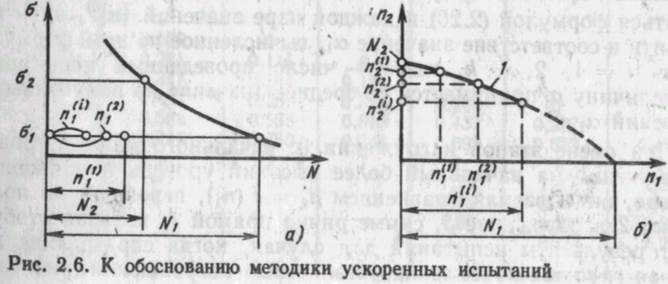
а) Ряс. 2.6. К обоснованию методики ускоренных испытаний

уровне напряжений до разрушения практически невозможно. В этом случае вначале выбирается некоторый уровень напряжений о₂ > Oj и производится обычное усталостное испытание на этом уровне напряжений. В результате получают соответствующее этому уровню напряжений число циклов до разрушения N_t. Затем переходят к испытаниям на двух уровнях напряжений a_t и а₂ (рис. 2.7). В первом эксперименте устанавливается амплитуда напряжений а_г и нагружение производится в течение некоторого относительно небольшого числа циклов п'". Затем переходят на уровень напряжений а₂ и испытание продолжают до поломки образца. В результате определяют число циклов нагружения пУ, соответствующее второму этапу испытаний. На диаграмме (Я|Ч-я₂) отмечают точку с координатами (п'", «УМ, которая изображает результат проведенного единичного испытания (см. рис. 2.6, б). Во втором эксперименте нагружение образца производится на том же уровне напряжений а_1? но уже в течение п'²' > л'" циклов, а доламывание вновь выполняют на уровне напряжений а₂. В результате определяется число циклов п₂²⁾, при котором происходит поломка образца на втором этапе испытаний. Вновь на диаграмме (п^п^) отмечают точку с координатами (п⁽[²⁾, «₂²⁾) (рис. 2.6, б). Продолжая такие испытания, получают зависимость n_z = f(rtj). На рис. 2.6, б эта зависимость показана в виде сплошной кривой /. Плавно продолжая эту кривую до пересечения с осью п_ь определяем искомое значение долговечности, соответствующее ожидаемому моменту разрушения образца на уровне напряжений а_г. На рис. 2.6, б это продолжение показано в виде штриховой линии.

Полученная в эксперименте зависимость п_г = f(n_t) обычно соответствует аналитическому соотношению (2.13). В этом случае для данного сочетания напряжений Oj и ст₂, реализованного в проведенном эксперименте, можно подобрать соответствующий параметр нелинейности ос. Это может быть сделано, например, стандартным методом наименьших квадратов. Определить этот параметр по полученным экспериментальным данным можно также вычислением среднего арифметического. Для этого следует воспользоваться формулой (2.20) и каждой паре значений {п['\ /г₂°} поставить в соответствие значение сс_ь вычисленное по этой формуле. Здесь ( == 1, 2, ..., k, где k— число проведенных испытаний. За величину ос принимается ее среднее значение из полученных kзначений а_;.