Кодирование речевых сигналов

Кодирование речевых сигналов

При рассмотрении цифровых методов обработки модель речевого сигнала часто представляют в виде эргодического случайного процесса.

Стационарный случайный процесс называют эргодическим, если при нахождении его моментных функций усреднение по ансамблю реализаций можно заменить усреднением по времени.

Момент n-го порядка случайной величины есть среднее значение n-ой степени случайной величины: .

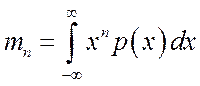Для использования статистических понятий при описании речевых сигналов необходимо оценить корреляционную функцию (или спектральную плотность мощности) и функцию плотности модели речевого сигнала.

Количественной характеристикой степени статистической связи двух сечений случайного процесса служит их ковариационная или корреляционная функция. Корреляционная функция – с вычетом постоянной составляющей.

Каждая отдельно взятая реализация случайного процесса представляет собой детерминированную функцию, к которой можно применить преобразование Фурье. Различные реализации одного случайного процесса будут иметь различные спектральные плотности. Статистически усредненной спектральной характеристикой случайного процесса является спектральная плотность мощности (СПМ), или спектр мощности. СПМ – вещественная функция, не содержащая информации и фазовых составляющих случайного процесса. СПМ не позволяет восстановить отдельные реализации случайного процесса. СПМ является четной неотрицательной функцией.

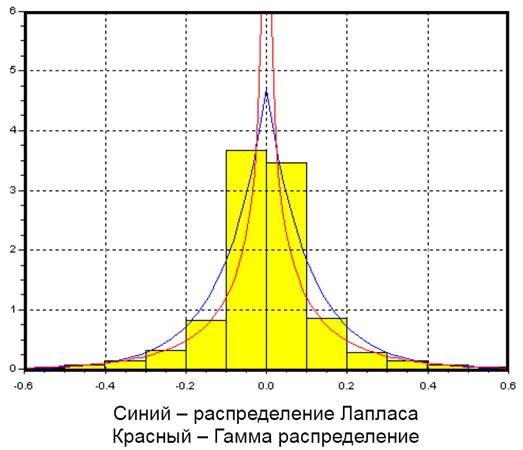
Функция плотности вероятности (ФПВ) речевого сигнала оценивается путем определения гистограммы по большому числу отсчетов речевого сигнала, т.е. по длительной временной реализации. Экспериментальные исследования показали, что хорошей аппроксимацией экспериментальной функции плотности вероятности служит гамма-распределение. Более простой аппроксимацией является распределение Лапласа.

Если частота дискретизации сигнала менее чем в 2 раза превышает верхнюю частоту спектра сигнала, то восстановление исходного сигнала оказывается невозможным. При этом возникают ошибки двух видов: связанные с усечением спектра исходного сигнала и связанные с наложением копий спектра, появляющихся в результате дискретизации. Идеальный фильтр нижних частот (ФНЧ) с прямоугольной АЧХ выделяет составляющие спектра, расположенные в интервале Найквиста, т.е. в диапазоне от 0 до . Частота Найквиста – это частота, равная половине частоты дискретизации. При этом отсекается часть спектра исходного сигнала в диапазоне от  до . В то же время в полосу пропускания идеального ФНЧ попадают составляющие от копии спектра, вызывающие эффект наложения спектров. Этих составляющих нет в исходном сигнале, что приводит к возникновению ошибок.

Для передачи дискретной последовательности отсчетов по цифровому каналу связи необходимо каждый отсчет проквантовать до конечного множества уровней. В результате кодирования каждому квантованному значению  ставится в соответствие кодовое слово . Аналогично декодер – устройство, которое последовательности кодовых слов ставит в соответствие последовательность квантованных отсчетов. Если кодовые слова не искажаются в канале передачи, то последовательность квантованных отсчетов на выходе декодера точно совпадает с последовательностью на входе кодера.

Чаще всего для кодирования квантованных отсчетов используется двоичная последовательность. С помощью ‑разрядного двоичного кодового слова можно представить  различных уровней квантования. Скорость передачи информации равна произведению разрядности кодового слова  на частоту дискретизации сигнала . Поскольку минимальная частота дискретизации определяется теоремой Котельникова, для снижения скорости передачи информации необходимо сокращать разрядность кодового слова.

В общем случае полагают, что отсчеты сигнала попадают в конечный интервал значений. Поскольку величина  не может быть бесконечно велика, то ее выбирают исходя из статистических свойств модели речевого сигнала в виде случайного процесса с распределением Лапласа. Таким образом, апертура квантователя пропорциональна среднеквадратическому отклонению речевого сигнала.

Апертура квантователя делится на интервалы, и всем отсчетам входного сигнала, попавшим в некоторый интервал, приписывается одно и то же значение.

Уровни квантования часто выбирают равномерно. Если начало отсчета приходится на середину между уровнями квантования, то квантователь называется квантователем с усечением, если на определенный уровень квантования – квантователем с округлением.

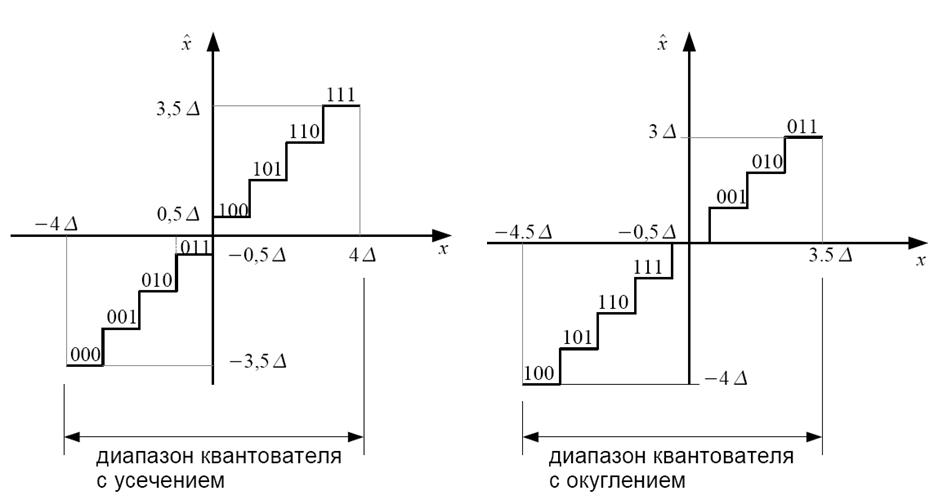
Если число уровней квантования равно целой степени 2, то квантователь с усечением имеет одинаковое количество положительных и отрицательных уровней, расположенных симметрично относительно начала координат. Квантователь с округлением имеет на один отрицательный уровень больше, зато обладает нулевым уровнем. Кодовые слова, соответствующие уровням квантования, можно рассматривать как номер уровня квантования со знаком.