При использовании методов разностного квантования квантованию подвергается разность между предсказанным и действительным значениями сигнала, или погрешность предсказания. Квантователь может быть адаптивным или неадаптивным, равномерным или неравномерным. Если параметры предсказателя соответствуют параметрам речевого сигнала, то дисперсия разностного сигнала будет меньше, чем дисперсия исходного сигнала, поэтому квантователь с заданным количеством уровней квантования обеспечит меньший шум квантования.
Величина выигрыша от использования разностного квантования зависит от корреляционной функции речевого сигнала. Один и тот же предсказатель не может быть оптимальным для различных дикторов, что обуславливает применение адаптивных предсказателей.
Простейший вид разностного квантования – дельта-модуляция. В таких системах частота дискретизации выбирается во много раз выше, чем частота в соответствии с теоремой Котельникова. В результате соседние отсчеты оказываются в большой степени коррелированными. При уменьшении периода дискретизации можно более точно предсказать текущий отсчет по предшествующим и, следовательно, уменьшить дисперсию погрешности предсказания. Поэтому даже «грубый» квантователь может дать хорошие результаты. В системе с дельта-модуляцией используется простой одноразрядный (двухуровневый) квантователь. Таким образом, скорость передачи при использовании дельта-модуляции численно равна частоте дискретизации.
Схема простейшей системы с дельта-модуляцией приведена на рисунке.
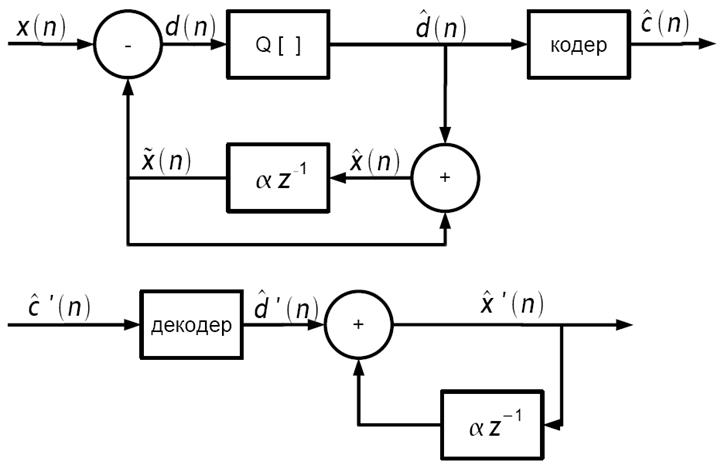
Квантователь имеет только два уровня
и фиксированный шаг квантования. Представленный на рисунке предсказатель
является одношаговым первого порядка. Положительный уровень квантования
соответствует ![]() , а отрицательный -
, а отрицательный - ![]() (см. рисунок).
(см. рисунок).
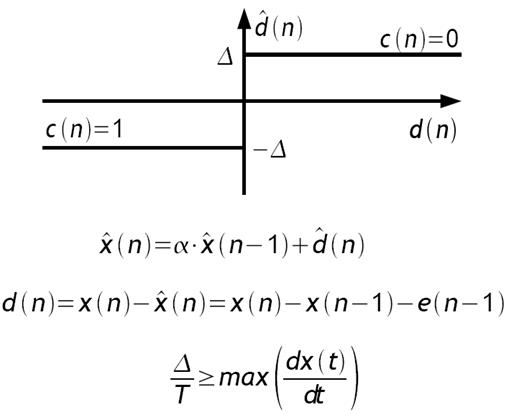
При ![]() значение
значение
![]() можно представить как разность первого
порядка сигнала
можно представить как разность первого
порядка сигнала ![]() (правильное написание
формулы
(правильное написание
формулы ![]() ). Разность может
рассматриваться как аппроксимация производной входного сигнала.
). Разность может
рассматриваться как аппроксимация производной входного сигнала.
Для того чтобы последовательность отсчетов ![]() возрастала так же быстро, как и последовательность
возрастала так же быстро, как и последовательность
![]() в области максимальной крутизны,
необходимо выполнение неравенства
в области максимальной крутизны,
необходимо выполнение неравенства
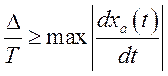 .
.
В противном случае восстановленный сигнал будет «отставать» от исходного. Данный вид искажений называется «перегрузкой по крутизне».
Поскольку максимальная крутизна ![]() ограничена
шагом квантования, то возрастание или убывание последовательности
ограничена
шагом квантования, то возрастание или убывание последовательности ![]() происходит по соответствующей ступенчатой
линии. Поэтому фиксированную (неадаптивную) дельта-модуляцию иногда называют
линейной дельта-модуляцией (ЛДМ).
происходит по соответствующей ступенчатой
линии. Поэтому фиксированную (неадаптивную) дельта-модуляцию иногда называют
линейной дельта-модуляцией (ЛДМ).
Шаг квантования определяет также и максимальную ошибку,
когда крутизна сигнала мала. При этом сигнал на выходе квантователя
представляет собой переменную последовательность нулей и единиц, что приводит к
флуктуации восстановленного сигнала вокруг постоянного уровня с размахом,
равным ![]() . Данный тип ошибок квантования называют
шумом дробления.
. Данный тип ошибок квантования называют
шумом дробления.
Для получения большого динамического диапазона необходимо иметь большой шаг квантования; в то же время для точного описания малых сигналов шаг квантования должен быть малым. В данном случае это относится к динамическому диапазону и амплитуде разностного сигнала (или производной аналогового сигнала). Выбор шага квантования, минимизирующего среднее квадратическое значение шума квантования, приведет к компромиссу между перегрузкой по крутизне и шумом дробления.
Исследования показали, что значение оптимального шага
квантования определяется согласно выражению 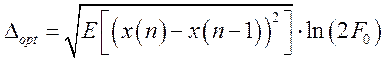 , где
, где ![]() ,
, ![]() ‑ частота
дискретизации,
‑ частота
дискретизации, ![]() ‑ частота
дискретизации согласно теореме Котельникова.
‑ частота
дискретизации согласно теореме Котельникова.
При удвоении ![]() , т.е. при удвоении
скорости передачи, значение отношения сигнал-(шум квантования),
соответствующее оптимальному шагу квантования, увеличивается на 9 дБ. Это
значительно больше, чем для ИКМ, где при удвоении скорости передачи увеличение
отношения сигнал-(шум квантования) составляет только 6 дБ.
, т.е. при удвоении
скорости передачи, значение отношения сигнал-(шум квантования),
соответствующее оптимальному шагу квантования, увеличивается на 9 дБ. Это
значительно больше, чем для ИКМ, где при удвоении скорости передачи увеличение
отношения сигнал-(шум квантования) составляет только 6 дБ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.