Модуль вращательного привода мехатронной системы, страница 3

Расчетное число зубьев гибкого колеса:

z^p_F=D_гп/m-5.88+1.96(h^*_a+c^*)=300/0.8-5.88+1.96(1+0.35)=371.77

Округляем до ближайшего меньшего целого числа z_F=370.

Число зубьев гибкого колеса:     z_С=z_F+j=370+2=372,  

где j – число волн деформации (зон зацепления).

Передаточное отношение волнового механизма:

u_в=z_C/(z_C-z_F)=372/(372-370)=186.

Момент нагружающий генератор волн деформаций:

М_г=М_вых/(u_в·η_в)=1558/(186·0.8)=10.47 Н·м.

Частота вращения генератора: n_г=n_вых·u_в=7·186=1302 об/мин

n_г≤[n_гп], 1302≤1600 условие работы гибкого подшипника выполнено.

Расчет геометрических размеров зубчатых
венцов гибкого и жесткого колес.

Коэффициенты смещения исходного контура (необходимы для исключения интерференции головок зубьев):

для гибкого колеса с внешними зубьями:

x_F=3+0.01·z_F=3+0.01·370=6.7;

для жесткого колеса с внутренними зубьями:

x_C=x_F-1+K_w·(1+5·10^-5·K_w·z_F)=6.7-1+1.2·(1+5·10^-5·1.2·370) = 6.927,

где K_w – коэффициент радиальной деформациигибкого колеса.

Диаметры колес:

делительные диаметры:

d_F=m·z_F=0.8·370=296 мм

d_С=m·z_С=0.8·372=297.6 мм

диаметры вершин:

d_aF=d_F+2·(x_F+K_F)·m=296+2·(6.7+0.4)·0.8=307.36 мм

d_aC=d_C+2·(x_C-h^*_a)·m=297.6+2·(6.927-1)·0.8=310.283 мм

диаметры впадин:

d_fF=d_F+2·(x_F-h^*_a-c^*)·m=296+2·(6.7-1-0.35)·0.8=304.56 мм

d_fC=d_aC+2·h_C=310.283+2·1.4=313.083 мм,

где h_C=(h^*_a+c^*+K_F)·m=(1+0.35+0.4)·0.8=1.4 мм – высота зуба жесткого колеса,

K_F -·коэффициент, характеризующий глубину захода зубьев колес.

Толщина стенки гибкого колеса под зубьями:

δ_сз=0.01·d_F=0.01·296=2.96 мм – упрощенная зависимость,

δ_сз=m·[0.5·z_F+x_F-(h^*_a+c^*)]-0.5·D_гп=0.8·[0.5·370+6.7-(1+0.35)]-0.5·300=2.28 мм – более точная.

Расчет конструктивных размеров гибкого и жесткого колес.

b_WF=0.2·d_F=0.2·296=59.2 мм – ширина зубчатого венца гибкого колеса;

b_WС=b_WF+3=62.2 мм – ширина зубчатого венца жесткого колеса;

l_ст=0.9·d_F=0.9·296=266.4 мм – длина стакана гибкого колеса,

b₁=0.054·d_F=0.054·296=15.984 мм – ширина пояска , выступающего за край зубчатого венца гибкого колеса (для снижения перекоса зубьев),

δ_с=0.78·δ_сз=0.78·2.28=1.778 мм – толщина стенки стакана гибкого колеса,

h_об=0.176·d_С=0.176·297.6=52.378 мм – толщина обода жесткого колеса под зубьями.

5.  Проектирование планетарной передачи

Требуемое передаточное отношение планетарного механизма:

u^т_пл=n_вх/n_вых=n_д/n_г=7600/1302=5.837

Ориентировочные значения передаточных отношений быстроходной и тихоходной ступени планетарного механизма:

u_ag=0.5(u^т_пл-1)=0.5(5.837-1)=2.418,

u_gb=(u^т_пл-1)/u_ag=(5.837-1)/2.418=2.

Момент нагрузки  воспринимаемый одним зацеплением на шестерне быстроходной ступени: M_1а=M_вх/n_w=1.812/3=0.604 Н·м, где

М_вх = М_вых / h_пл×n_w = 10.47/ 0.99×3=1.812 – момент на входном валу планетарного механизма, n_w – число сателлитов.

Максимальное значение  числа зубьев шестерни для быстроходной ступени:

(z_мах)_а=c(u+1)/u=35(2.418+1)/2.418=49,475,

где с – коэффициент зависящий от характера работы передачи.

Принимаем z_а=49

Диаметр начальной окружности шестерни а:

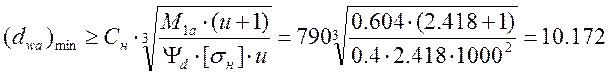
где ψ_d – коэффициент ширины зубчатого венца шестерни, [σ_н] – допускаемое контактное напряжение.

Проектное значение модуля передачи:

m=(d_wa)_min/z_a=10.172/ 49=0.208

принимаем m=0.6.

Число зубьев колеса b: z_b=z_a(u^T_пл-1)=49(5.837-1)=237,013

принимаем z_b=237

Число зубьев колеса g: z_g=(z_a-z_b)/2=(237-49)/2=94

Габаритные и конструктивные условия.

d_а=m·z_а=0.6·49=29,4≥2·d_дв=25 29.4>25 т.е. на вал электродвигателя можно закрепить центральное колесо а.

Передаточные отношения отдельных ступеней механизма:

u_ag=94/49=1,918,

u_gb=237/94=2.521.

Передаточное отношение всего механизма:u=1,918·2.521=4,835.