Безвихревое течение идеальной жидкости. Четырёхугольный кубичный элемент. Решение системы линейных уравнений с итерационным уточнением

1.Введение.

   Основная   цель  выполнения   курсовой   работы   заключается в закреплении теоретических и практических знаний.

   В данной работе освещены следующие вопросы:

  ¾ безвихревое течение идеальной жидкости,

  ¾ четырёхугольный кубичный элемент.  

  ¾ решение системы линейных уравнений с итерационным уточнением.

   При   формальном   подходе  задача течения идеальной жидкости заключаются   в применении   численного   метода   отыскания   решения    уравнения Пуассона:

,

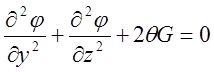где      ¾ функция   напряжения   Прандтля;

           ¾ относительный   угол   закручивания;

           G ¾ модуль   сдвига.

    Решение задачи течения осуществляется с помощью применения методов, которые легко можно запрограммировать. Это метод конечных элементов, метод прямых и обратных итераций и прочие.

    В практической части курсовой работы рассматривается кубичный четырёхугольный элемент. В данном разделе демонстрируется техника высокоточных элементов. Известно, что во многих случаях в реальной конструкции наблюдается искажение исходной геометрии. В этом случае уменьшить погрешность вычислений можно с помощью применения данного элемента.

    В последнем разделе работы рассмотрена подпрограмма RSLMC, предназначенная для решения системы линейных уравнений вида

AC=B,

где A ¾ неособенная матрица коэффициентов системы,

      B ¾ вектор правых частей,

      Х ¾ вектор, который необходимо найти в результате решения.

1.1.Плоское безвихревое течение несжимаемой жидкости.

Безвихревое течение идеальной  рассматривается достаточно широко, потому что при этом могут быть решены многие физические задачи , такие , как обтекание углов, плотин , несущих поверхностей самолёта , различных конструкций. Идеальное безвихревое течение  представляет собой некоторое приближение к реальному физическому процессу . При этом предполагается , что между жидкостью и обтекаемой поверхностью нет трения (идеальная жидкость) и вращательное движение жидкости отсутствует (безвихревое течение).

  Задачи , включающие рассмотрение безвихревого течения , могут быть решены с помощью метода конечных элементов.

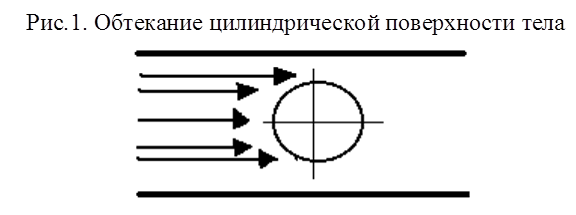
  Рассмотрим плоское стационарное движение несжимаемой жидкости рис.1.

  При плоском движении все частицы жидкости получают перемещения, параллельные некоторой плоскости, которую примем за плоскость (xoy) , причем во всех параллельных плоскостях движения тождественны. Будем рассматривать поэтому лишь движение в плоскости (xoy). Каждая линия в таком плоском движении, проведенная в плоскости (xoy), является на самом деле направляющей цилиндрической поверхности с образующими, перпендикулярными к плоскости (xoy). Контур обтекаемого тела представится некоторой линией в плоскости, хотя на самом деле происходит обтекание бесконечного цилиндрического тела. Все значения расходов жидкости, сил, приложенных к обтекаемым телам, и т. д. будем относить к единице длины в направлении перпендикуляра к плоскости (xoy), т. е. в направлении оси oz, которая на рисунках опускается.

  В рассматриваемом случае задача сводится к решению задачи об интегрировании при тех или иных граничных условиях  уравнения Лапласа, которое для плоского случая имеет вид

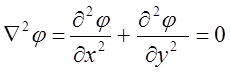    (1)

Из уравнения неразрывности (несжимаемости)

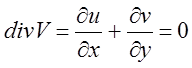
следует, что всегда можно найти функцию Y(х, у), тождественно удовлетворяющую уравнению (1) и связанную с проекциями скорости u и v равенствами

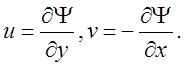                (2)

Функция Y(х, у) имеет простой гидродинамический смысл. В самом деле , напишем дифференциальное уравнение линий тока, в случае плоского движения имеющее вид

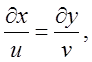
и подставим в него значения проекций скорости по (2); тогда будем иметь

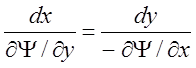
и

  

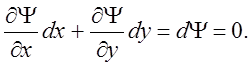
  Из последнего равенства следует, что функция Y сохраняет постоянные значения вдоль линий тока; иными словами, семейство линий уровня функции

           (3)