Безвихревое течение идеальной жидкости. Четырёхугольный кубичный элемент. Решение системы линейных уравнений с итерационным уточнением, страница 2

соответствующих различным значениям С, представляет собой совокупность линий тока. Функция Y(х, у) в связи с этим называется функцией тока. Для выяснения кинематического смысла функции тока рассмотрим в плоскости течения две бесконечно близкие линии тока одну—проходящую через точку М₀ , с соответствующим значением функции тока Y_{0 ,}, вторую — через точку М₁ со значением функции тока  (рис.2).

                   

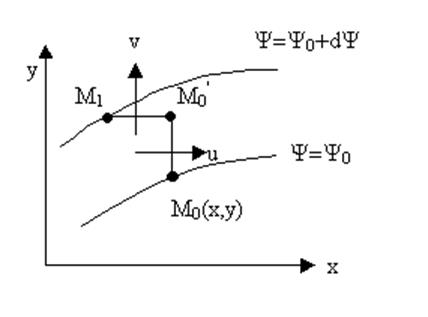
Рис.2. Иллюстрация кинематического смысла функций тока.

 Часть жидкости, находящаяся между цилиндрическими поверхностями, перпендикулярными к плоскости рисунка и имеющими линии тока в качестве направляющих, образует элементарную трубку тока, которую будем ограничивать плоскостью рисунка и параллельной ей плоскостью, находящейся на расстоянии единицы длины от плоскости рисунка. В случае плоского движения указанный только что образ трубки тока представляется областью, заключенной между двумя линиями тока в плоскости движения жидкости. Это пояснение надо иметь в виду в дальнейшем.

Замечая (рис. 2), что элементарный секундный объемный расход жидкости dQ через любое сечение трубки тока не зависит от формы этогo сечения, выберем его в виде совокупности двух параллельных осям координат отрезков М₀М’₀=dy и М’₀M₁=-dx. Тогда, как это непосредственно следует из рисунка, выражение для dQ примет вид

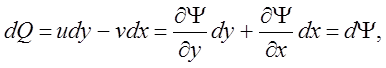
откуда следует выражение расхода сквозь конечную по поперечным размерам трубку (М₀М)

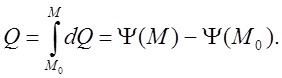           (4)

соответствующих различным значениям С, представляет собой совокупность линий тока.

  Условимся в дальнейшем одну какую-нибудь линию тока произвольно рассматривать как нулевую, полагая, что вдоль нее

Y(x,y)=0.

Это можно всегда сделать, так как, согласно системе равенств (2),функция тока определяется с точностью до аддитивной постоянной. Если принять такое условие, то значение константы в (3) на некоторой линии тока будет равно секундному объемному расходу жидкости сквозь сечение трубки тока, образованной этой линией тока и выбранной произвольно нулевой линией. Линии тока характеризуются также тем , что в перпендикулярном к ним направлении отсутствует течение жидкости .

  При обтекании тела идеальной жидкостью считается ,что жидкость не проникает в тело и не отходит от него , образуя пустоты. Это приводит к следующему условию на граничной поверхности: компонента скорости течения жидкости, нормальная к граничной поверхности, совпадает со скоростью поверхности в этом направлении. Для неподвижной границы приведенное условие означает отсутствие течения , перпендикулярного этой границе , поэтому на неподвижной границе перпендикулярная к ней компонента скорости течения равна нулю.

  Сопоставим выражения  проекций скорости через потенциал скоростей, которые в случае плоского движения сводятся к системе двух равенств

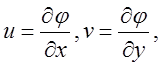          (5)

и выражения (2) тех же проекций через функцию тока Y будем иметь следующую систему соотношений:

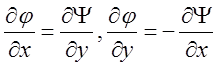.     (6)

  Задача о безвихревом течении может быть сформулирована с использованием потенциала скоростей. Дифференциальное уравнение примет вид

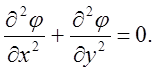            (7)   

При решении уравнения (7) с граничным условием

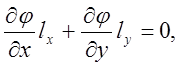
где l_x ,l_y –направляющие косинусы единичной нормали, возникает дополнительная трудность. Решение уравнения (7) не единственно . Матрица [К] системы сингулярна . Эта трудность может быть преодолена выбором одного узла и заданием значения j в этом узле . Так как скорости определяются дифференцированием функции j ,то значение j в выбранном узле всегда можно брать равным нулю. 

4. Литература

1. Сегерлинд Л.Д., ”Применение метода конечных элементов”, Москва: Мир, 1979год.

 2. Лойцянский П.Г., “Механика жидкости и газа”, Москва: Наука, 1973 год.

 3. Кудряшов И.А., Кушнер и др., “Программирование, отладка и решение задач на ЭВМ единой серии. Язык Фортран.”