Расчет моментов инерции движущихся инерционных масс привода. Определение приведенных к скорости вращения электродвигателя моментов статического сопротивления для двух режимов работы электродвигателя, страница 4

Принимаем допущение о линейности механических (естественных и искусственных) характеристик на всём допустимом диапазоне изменении их статически и динамических нагрузок. В этом случае решение уравнения движения электропривода в одномассовой жёсткой системе 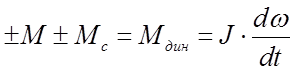 имеет вид:

,

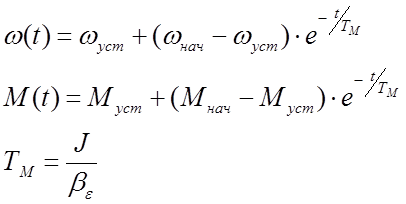где  − начальное значение угловой скорости и момента двигателя;

 − установившееся значение угловой скорости и вращающего момента двигателя по окончанию переходного процесса;

 − время;

 − электромеханическая постоянная времени;

 − суммарная жёсткость механической характеристики двигателя и механизма, при  тогда .

Значение  определяем по формуле:

.

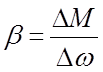Воспользуемся рисунком 7 и определим  для первой пусковой ступени:

;

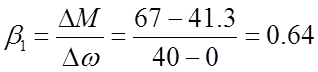Соответственно значения электромеханической постоянной:

;

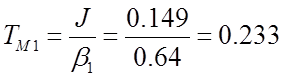Длительность переходного процесса первой ступени:

,

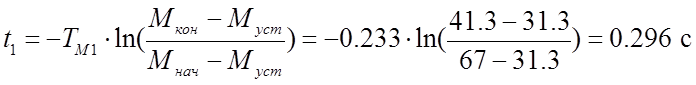где ;

;

.

Все данные сведём в таблицу 5.

Таблица 5 Значения жёсткости, электромеханической постоянной и длительности переходного процесса для каждой ступени

Ступень	1	2	3
	40	25	16
	25.7
	0.64	1.03	1.60
	0.233	0.145	0.093
	0.296	0.184	0.118

Найдём значения круговой частоты и момента для первой пусковой ступени для различного времени.

;

.

, тогда ;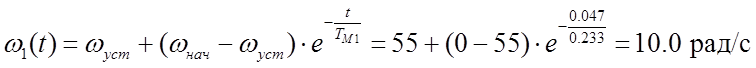

.

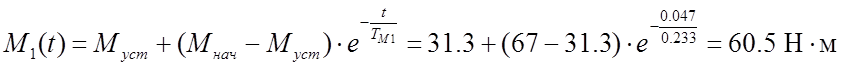Для оставшихся ступеней проделаем тоже самое и полученные результаты занесём в таблицу 6.

Таблица 6 Значения момента и круговой частоты от времени

Ступень		Длительность переходного процесса
1	0.233	0.296	0.074	14.9	57.3
			0.148	25.8	50.2
			0.222	33.8	45.1
			0.296	39.5	41.3
2	0.145	0.184	0.046	49.2	57.3
			0.092	56.0	50.2
			0.138	60.9	45.1
			0.184	64.4	41.3
3	0.093	0.118	0.0295	70.7	57.3
			0.059	74.9	50.2
			0.089	77.9	45.1
			0.118	80.1	41.3

Полное время разгона будет равно .

Полученные зависимости изображены на рисунке 7.

Рассчитать и построить графики механических переходных процессов  электропривода грузоподъёмной лебёдки при динамическом торможении в конце подъёма груза по характеристике, рассчитанной в пункте 7 задачи 1, до полной остановки груза.

Аппроксимируем характеристику динамического торможения тремя отрезками. Определим жёсткость характеристики на каждом из участков, электромеханическую постоянную и время переходного процесса.

Рассмотрим участок 1−2:

Жёсткость определяется как тангенс угла наклона касательной:

 .

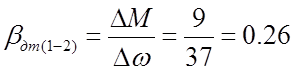Найдём значение электромеханической постоянной времени:

.

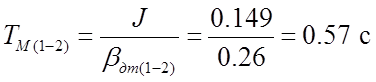Найдём время переходного процесса:

 

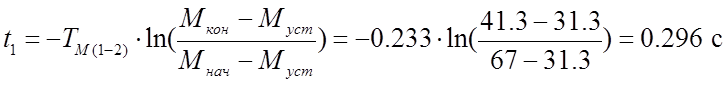
Для оставшихся участков 2−3 и 3−4 сделаем тоже самое, и полученные результаты занесём в таблицу 7.

Таблица 7 Значения жёсткости, электромеханической постоянной и длительности переходного процесса для каждой ступени

Ступень	1	2	3
	34	26	37
	9	19.5	51.5
	0.26	0.75	1.51
	0.57	0.2	0.1
	0.052	0.047	0.118

Время торможения до полной остановки будет равно:

.

Найдём значения круговой частоты и момента для первой пусковой ступени для различного времени.

;

.

, тогда;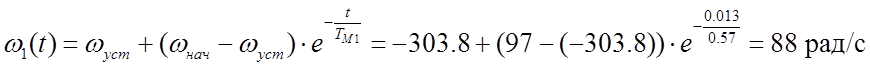

.

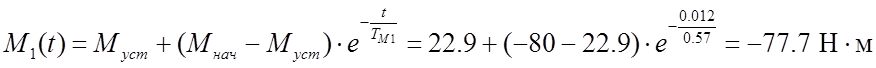Полученные значения занесём в таблицу 8.

Таблица 8 Значения момента и круговой частоты от времени

Ступень		Длительность переходного процесса
1	0.57	0.052	0.013	88	-77.7
			0.026	79.1	-75.4
			0.039	70.5	-73.2
			0.052	62	-71
2	0.2	0.047	0.012	52.9	-65.5
			0.024	46.2	-60.4
			0.036	39.9	-55.5
			0.047	34.4	-51.3
3	0.1	0.118	0.03	27.5	-41.1
			0.06	21.4	-32.2
			0.09	16.2	-24.5
			0.118	12	-18.3