Лебёдка вращается под действием силы тяжести груза, т. е сила тяжести совершает работу, часть которой расходуется в механизме, часть теряется в редукторе, остальная работа расходуется на вращение двигателя, работающего в режиме генераторного торможения:
![]() ,
,
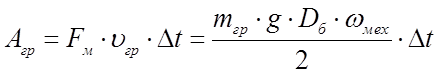 .
.
Зная, что ![]() , получим:
, получим:
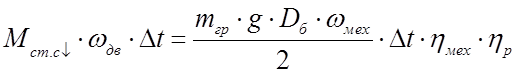 ,
,
учитывая, что 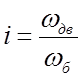 , найдём
, найдём
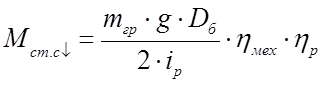 .
.
Подставим численные значения:
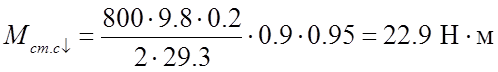 .
.
Пункт 3
Построить естественные скоростные и механические характеристики электродвигателя. Указать на них величину установившихся скоростей вращения двигателя при подъёме и спуске груза. Определить по ним соответствующие линейные скорости подъёма и опускания груза
Для расчёта и построения статических механических характеристик АД рекомендуется использовать уравнения, полученные на основе упрощенной Г–образной схемы замещения и позволяющие получить достаточную (в пределах 5%) для инженерных расчётов точность.
Приведём активные
сопротивления обмоток статора и ротора данных при ![]() к соответствующим сопротивлениям
при
к соответствующим сопротивлениям
при ![]() :
:
![]() ,
,
![]() ,
,
где ![]() − температурный коэффициент
сопротивления для меди;
− температурный коэффициент
сопротивления для меди;
![]() −
разница температур меди.
−
разница температур меди.
Запишем формулу для определения электромагнитного момента:
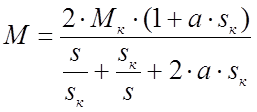 ,
,
здесь 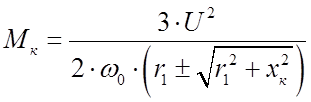 − критический (максимальный)
момент;
− критический (максимальный)
момент;
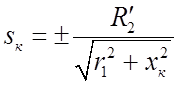 −
критическое скольжение соответствующее максимальному моменту.
−
критическое скольжение соответствующее максимальному моменту.
![]() −
скольжение;
−
скольжение;
![]() −
приведённое к обмотке статора суммарное активное сопротивление фазной обмотки
ротора;
−
приведённое к обмотке статора суммарное активное сопротивление фазной обмотки
ротора;
![]() −
приведённое к обмотке статора активное сопротивление фазной обмотки ротора;
−
приведённое к обмотке статора активное сопротивление фазной обмотки ротора;
![]() −
суммарное индуктивное сопротивление;
−
суммарное индуктивное сопротивление;
![]() −
индуктивное сопротивление фазной обмотки ротора, приведённое к обмотке статора;
−
индуктивное сопротивление фазной обмотки ротора, приведённое к обмотке статора;
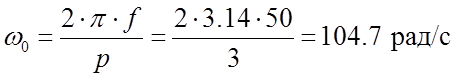 −
угловая скорость вращения ротора;
−
угловая скорость вращения ротора;
![]() −
число пар полюсов двигателя.
−
число пар полюсов двигателя.
Для расчёта и построения статических механических
характеристик АД используя эти уравнения при номинальных значениях (![]() )
и отсутствии добавочного сопротивления в цепи ротора
)
и отсутствии добавочного сопротивления в цепи ротора ![]() . Вначале рассчитываем значения
. Вначале рассчитываем значения ![]() . Затем, задаёмся значениями
скольжения
. Затем, задаёмся значениями
скольжения ![]() в пределах
в пределах ![]() до
до ![]() и
рассчитываем текущее значение электромагнитного момента
и
рассчитываем текущее значение электромагнитного момента ![]() .
.
Для отрицательных скольжений ![]() при расчёте значений
при расчёте значений ![]() и
и ![]() принимается
знак (–).
принимается
знак (–).
Определим критическое скольжение:
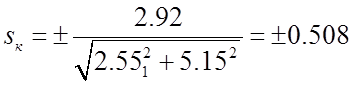 .
.
Определим максимальный (критический) момент:
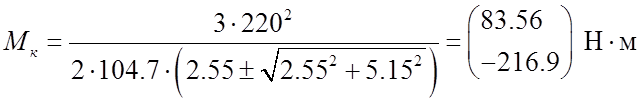 .
.
Определим
электромагнитный момент для скольжения ![]() :
:
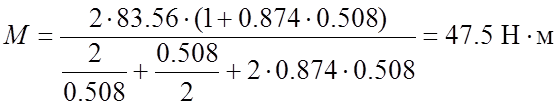 ,
,
где 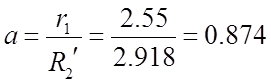 .
.
Угловая скорость определяется по формуле:
![]() .
.
Определим ![]() для
для ![]() :
:
![]() .
.
Занесём в таблицу 1 значения электромагнитного момента в зависимости от скольжения.
Таблица 1 Зависимость электромагнитного момента от скольжения
|
|
-0.5 |
-0.45 |
-0.4 |
-0.35 |
-0.3 |
-0.25 |
-0.2 |
-0.15 |
-0.1 |
|
|
-217 |
-214 |
-206.2 |
-192.6 |
-172.8 |
-147..4 |
-118 |
-86.4 |
-55 |
|
|
157.1 |
151.8 |
146.6 |
141.3 |
136.1 |
130.9 |
125.6 |
120.4 |
115.2 |
|
|
0.1 |
0.2 |
0.6 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
2 |
|
|
39.1 |
63.1 |
82.7 |
71.7 |
65.7 |
60.2 |
55.4 |
51.2 |
47.5 |
|
|
94.2 |
83.7 |
41.9 |
0 |
-21 |
-41.9 |
-62.8 |
-83.8 |
-104.7 |
Построим естественную механическую характеристику асинхронного двигателя. Она показана на рисунке 3.
Номинальная угловая скорость вращения двигателя:
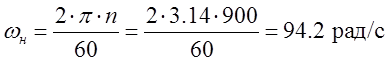
По характеристике определяем:
Номинальный момент:
![]() .
.
Установившаяся угловая скорость при спуске:
![]() .
.
Установившаяся угловая скорость при подъёме груза:
![]() .
.
Найдём линейные скорости при подъёме и при спуске груза:
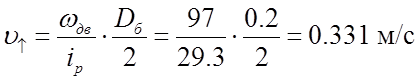 ;
;
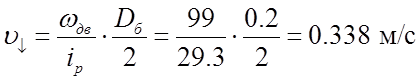 .
.
Рассчитаем величину тока статора ![]() и предварительно найдём значения
тока ротора,
и предварительно найдём значения
тока ротора, ![]() и номинальный ток
намагничивания
и номинальный ток
намагничивания ![]() номинальное значение
тока намагничивания принимают равным реактивной составляющей тока холостого
хода
номинальное значение
тока намагничивания принимают равным реактивной составляющей тока холостого
хода![]() .
.
Номинальный ток намагничивания:
![]() .
.
Значение приведённого тока ротора:
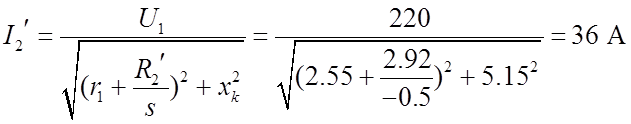 .
.
Синус угла сдвига между
фазной эдс ротора и фазным током ротора для ![]() :
:
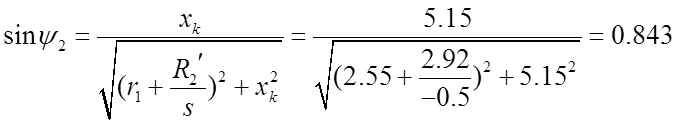 .
.
Ток статора:
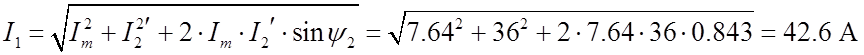 .
.
Занесём в таблицу 2 значения тока статора, приведённого тока ротора и в зависимости от скольжения.
Таблица 2 Значения тока статора, приведённого тока ротора в зависимости от скольжения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.