Анализ системы автоматического управления. Проверка заданной САУ на устойчивость с помощью критерия Михайлова. Проверка устойчивости линейной САУ с помощью критерия Найквиста

1. Анализ системы автоматического управления

Исходные данные.

Структурная схема (рис №1):

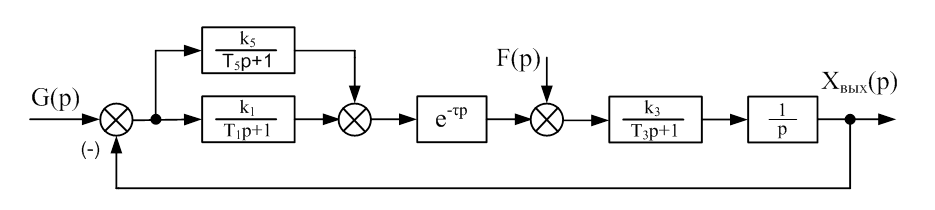
Рис.1 Исходная структурная схема.

Значения параметров структурной схемы:

k=0.25                       T=0.08                       τ=0.015

k₁=12                         T₁=0.04

k₂=1.4                        T₂=0.055

k₃=6.0                        T₃=0.035

k₅=1.82                     T₄=0.015

                                    T₅=0.25

1.1 Исследование заданной САУ на устойчивость двумя методами.

Введем обозначения передаточных функций каждого звена:

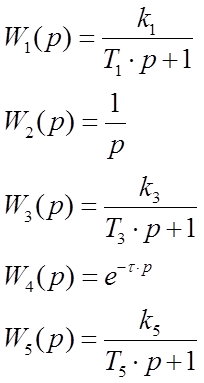
В заданной системе имеется параллельное соединение двух звеньев,  и ,преобразуем его в эквивалентное.

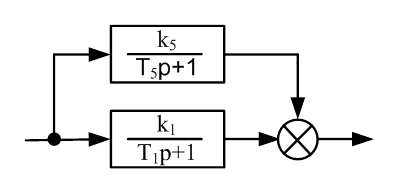
Рис.2 Параллельное соединение звеньев исходной САУ.

Общий вид формулы эквивалентного преобразования параллельных звеньев имеет вид (1, с 176):

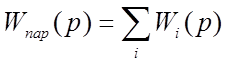
В нашем случае мы получим:

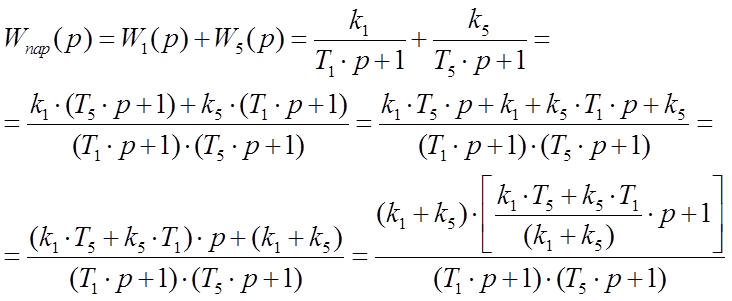
Сделаем замену и найдем вид эквивалентного звена:

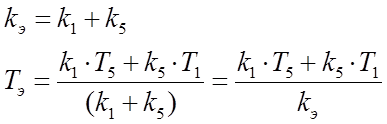
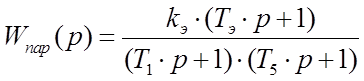
Полученное звено можно представить в виде последовательного соединения трех звеньев:

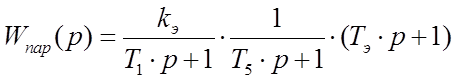
Введем обозначения передаточных функций:

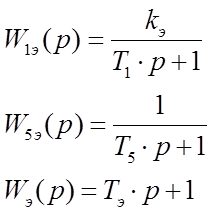
В результате получим структурную схему следующего вида (рис №3):

Рис.3 Преобразованная структурная схема исходной САУ.

а) Так как звенья полученной системы соединены последовательно, то передаточная функция системы в разомкнутом состоянии по управляющему воздействию будет иметь следующий вид (1, с 176):

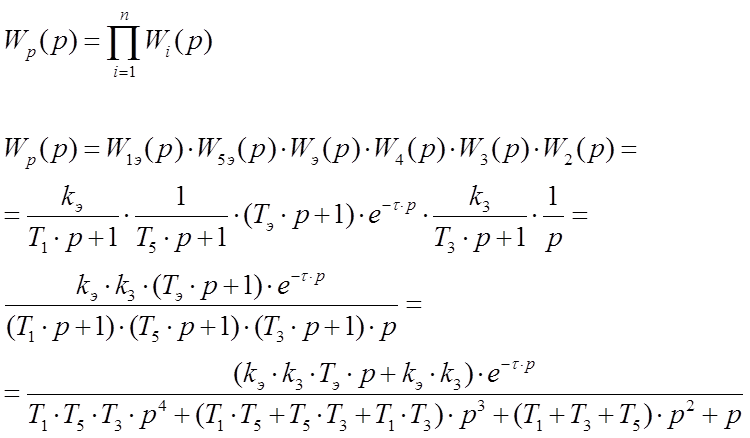
Вычислим значения всех указанных величин в передаточной функции:

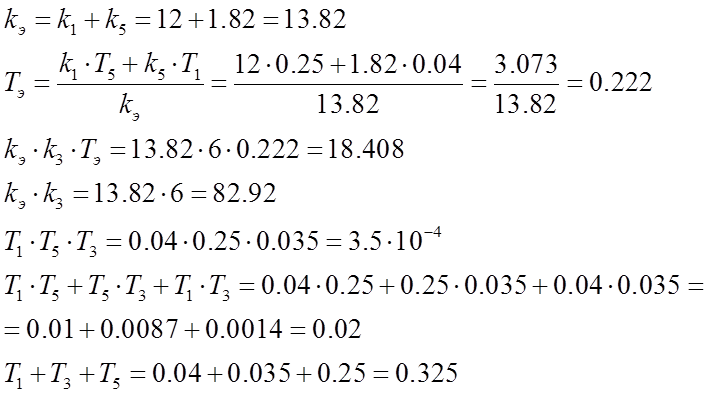
Подставим эти значения, найдем окончательный вид передаточной функции системы по управляющему воздействию в разомкнутом состоянии:

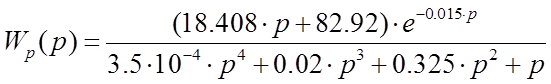
б) Найдем передаточную функцию системы по управляющему воздействию в замкнутом состоянии (1, с 177):

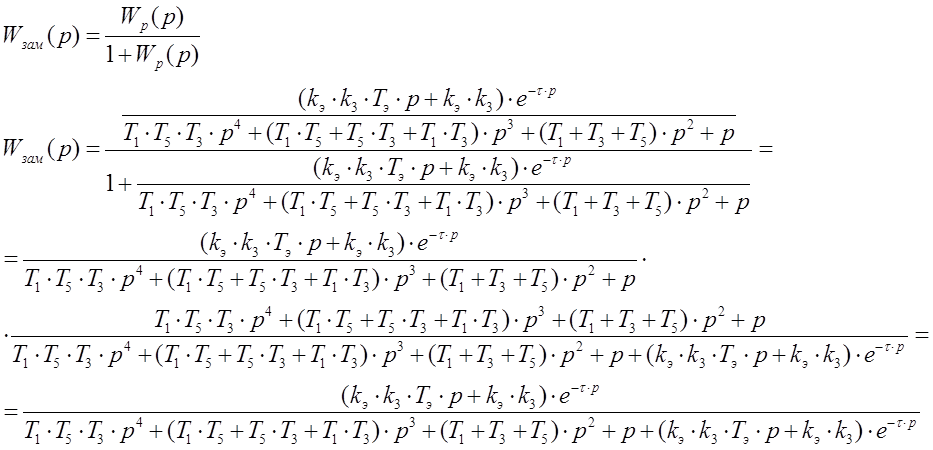
Подставим значения величин подсчитанных в пункте а) и найдем вид :

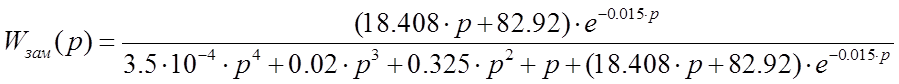
в) Найдем передаточную функцию ошибки по управляющему воздействию (1, с 164)

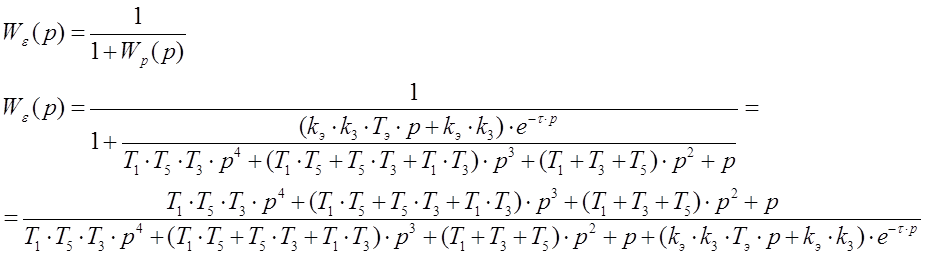
Подставим значения

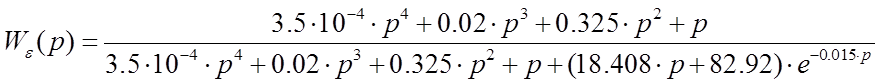
г) Характеристическим уравнением системы в замкнутом состоянии является знаменатель этого уравнения, приравненный к нулю. В нашем случае характеристическое уравнение имеет вид:

Проверка заданной САУ на устойчивость с помощью критерия Михайлова.

Критерий устойчивости Михайлова, принадлежит к частотным критериям и позволяет оценивать устойчивость системы по виду годографа, который может быть построен, исходя из характеристического уравнения.

Формулировка критерия устойчивости Михайлова:

Для устойчивости системы в замкнутом состоянии, необходимо и достаточно, чтобы вектор , описывающий своим концом кривую Михайлова, при изменении частоты  от 0 до , начав своё движение с положительной действительной оси и вращаясь против часовой стрелки, последовательно проходя n квадрантов, нигде не обращаясь в нуль. (1, с 213)

Характеристическое уравнение заданной САУ в замкнутом состоянии имеет вид:

Приравняем этот многочлен к нулю и перейдем в комплексную плоскость, то есть, заменим p на . В результате получим:

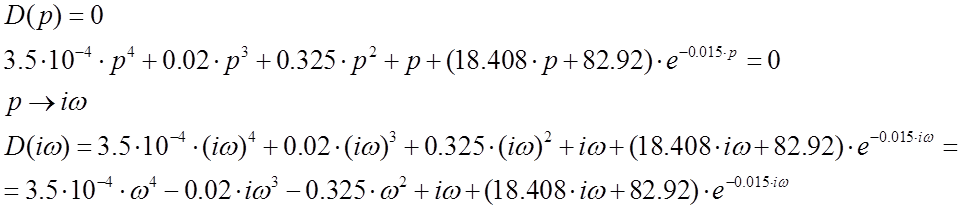
Данное уравнение позволяет построить годограф Михайлова на комплексной плоскости изменяя ω от 0 до +∞ и по его виду судить об устойчивости САУ.

Для построения годографа на комплексной плоскости представим многочлен  в виде суммы двух слагаемых. Для этого воспользуемся формулой Эйлера:

Запишем отдельно  и :

Подставляем в полученные формулы значения частоты ω, начиная с нуля и полученные результаты сводим в таблицу:

Таблица №1. Значения  и .

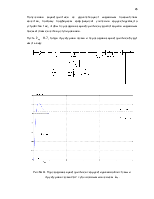
По данным таблицы строим годограф Михайлова (рис №4).

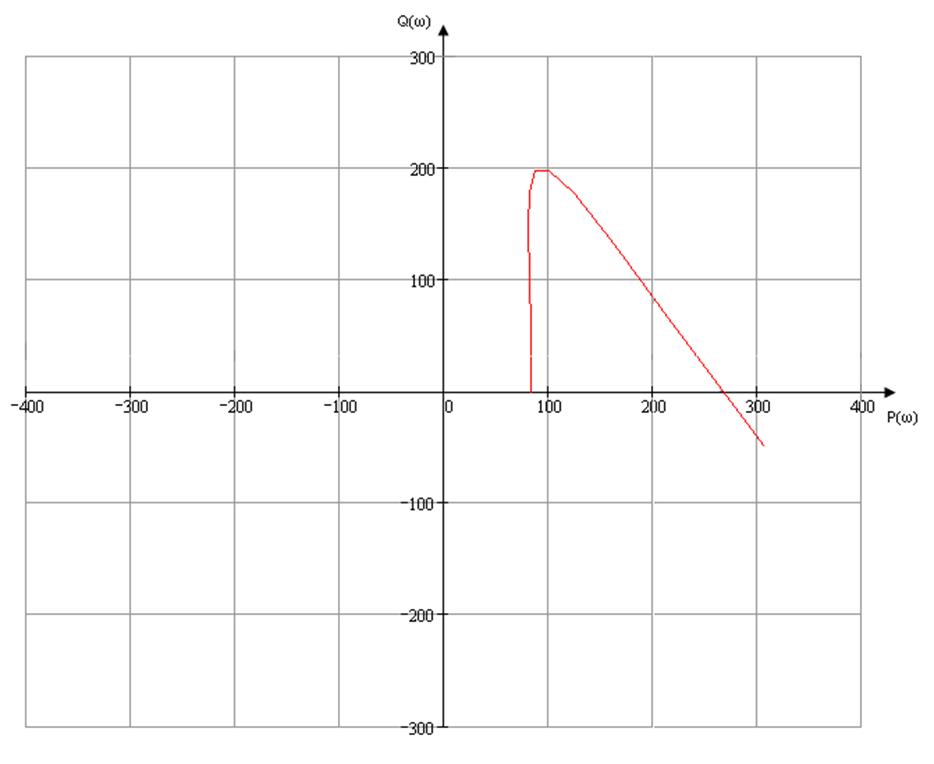
Рис.4 Годограф Михайлова

По виду годографа Михайлова видно, что заданная САУ не устойчивая, т.к. он не удовлетворяет условиям критерия Михайлова.

Проверка устойчивости линейной САУ с помощью критерия Найквиста.

Критерий Найквиста – это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы в зависимости от вида амплитудно−фазовой (АФХ) или логарифмических частотных характеристик (ЛЧХ) разомкнутой системы.

Помимо исследования устойчивости по виду указанных характеристик можно оценить и некоторые качественные показатели замкнутой системы, например, запас устойчивости. Более того, появляется возможность указать, как и за счет каких средств неустойчивая замкнутая система может быть сделана устойчивой и как можно повысить качество устойчивой замкнутой системы.

Формулировка критерия устойчивости Найквиста в логарифмических координатах: если разомкнутая система устойчива, то для устойчивости заданной САУ необходимо и достаточно, чтобы ЛФЧХ при изменении частоты  от 0 до , пересекала линию 180^о справа от частоты среза.

Воспользуемся полученной ранее структурной схемой заданной САУ после преобразования параллельного соединения, но без обратной связи. Она имеет вид:

Рис.5 Преобразованная исходная структурная схема без обратной связи.

Определим частоты сопряжения типовых звеньев: