Энергия элетромагнитного поля

3 ЭНЕРГИЯ ЭЛЕТРОМАГНИТНОГО ПОЛЯ

Электромагнитное поле обладает энергией и переносит ее, в системах

связи электромагнитное поле используется для передачи информации, при этом переносится и энергия. Изменяясь, ЭМП может отдавать свою энергию какому-либо неэлектромагнитному процессу или отбирать ее. Выделим область V, пусть в момент времени t заключенная в ней энергия ЭМП есть W(t). При этом может оказаться, что

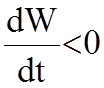 или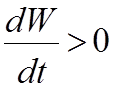  

Первое означает, что энергия поля в V изменяется в результате

поглощения в среде или отдачи ее в полезную нагрузку, причем энергия поля превращается в иные формы (например, необратимо переходит в тепло). Второе означает возрастание энергии, связанное с действием источников энергии (генерация), регенеративными процессами в среде, либо с притоком энергии извне. Основную информацию об ЭМП получают, изучая превращение энергии поля в иные формы. Специфические особенности различных превращений энергии не рассматриваются в курсе электродинамики. Предметом данного раздела является общее описание баланса энергии ЭМП, ее распределения и движения.

             Уравнение баланса энергии. Исходя из общих физических соображений, уравнение баланса активных энергий для мгновенных значений поля будет выглядеть таким образом:

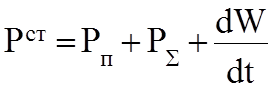,                                                       (3.1)

             где Р^СТ - мощность сторонних источников, находящихся в объеме V,

                   Р_П – мощность тепловых потерь, то есть мощность, расходуемая на нагрев проводников, резисторов, любых сред имеющих s¹0,

      Р_S - мощность, исходящая из объема, мощность излучения,

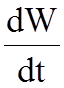- мощность, определяющая изменение от времени, возрастание или уменьшение энергии.

             Аналогичное уравнение можно получить из уравнений Максвелла следующим образом: умножим первое уравнение на , второе на и из второго вычитаем первое:

;     ;

;

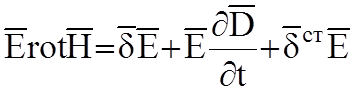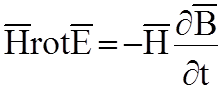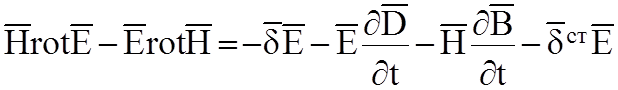В левой части .

Обозначим , это вектор Пойтинга. В результате имеем:

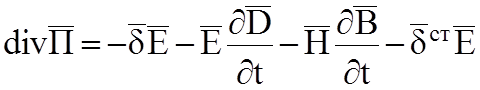
Умножим на (-1) и перенесем в левую часть  :

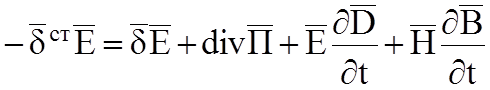
Это уравнение в дифференциальной форме, то есть для бесконечно малого объема, для точки.

Для всего объема проинтегрируем по объему V:

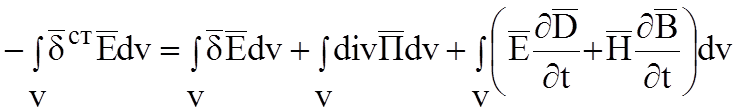
Произведем замены:

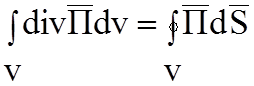по Т. Остроградского – Гаусса

;

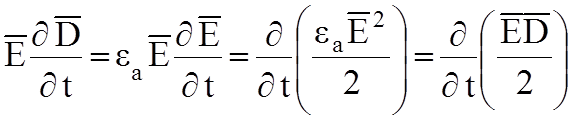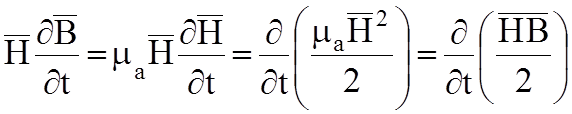
В результате окончательный вариант:

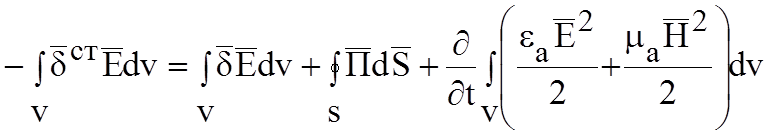           (3.2)

             Это есть теорема Умова – Пойтинга для объема. Рассмотрим физический смысл интегралов. Произведение  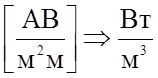   имеет размерность плотности мощности, а интеграл 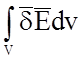 - есть мощность, которая тратиться в объеме на создание и поддержание токов проводимости в среде с s¹0: так как . Эта мощность в конечном итоге превращается в тепло. Очевидно, что остальные интегралы также имеют размерность мощности. В правой части уравнения потребители мощности, в левой части источник мощности сторонний. Сравнивая с уравнением (3.1) можем записать так:

             ;  

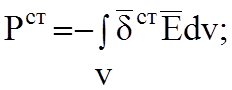
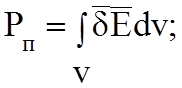
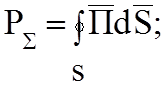
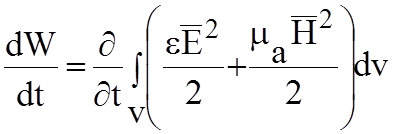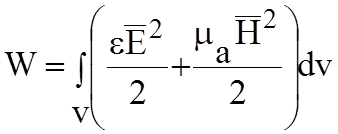
Мощность сторонних источников Р^СТ >0, отсюда скалярное произведение , это значит что векторы и  направлены навстречу и электрические заряды в источнике двигаются против сил электрического поля и двигаются они за счет сил неэлектрического происхождения (механических, химических). Это объясняет знак «минус» для Р^СТ.

             Рассмотрим мощность излучения 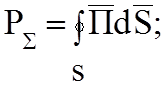это мощность уходящая из объема через поверхность S, это поток мощности, тогда вектор Пойтинга есть плотность потока мощности, имеет размерность Вт/м². Итак, вектор  определяет поток энергии, проходящей через единицу площади (м²) в единицу времени (1 сек) перпендикулярно площади. Эта величина имеет размерность мощности и называется потоком энергии. Это количественная характеристика. Теперь, что указывает направление вектора . Если рассматривать мгновенное значение , то он указывает направление движения энергии в данный момент времени, при рассмотрении во времени за период колебания или больше, то указывает направление переноса энергии. Направление  определяют вектором  и , связанные между собой.

                                                                            (3.3)

             Это векторное произведение  и , и вектор есть вектор перпендикулярный векторам  и . Иначе говоря, векторы , , , составляют правую тройку взаимно ортогональных векторов.