Энергия элетромагнитного поля, страница 2

             Последний интеграл в (3.2) есть энергия в объеме 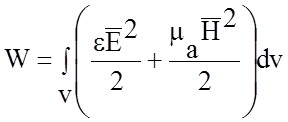 , а подинтегральное выражение плотность энергии w :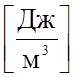

                                       ;   ;  

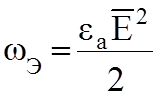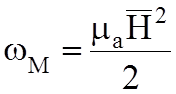
Энергия в ЭМП распределена между электрическим и магнитным полями и в зависимости от момента времени может находиться полностью в электрическом поле или в магнитном поле, хотя запас энергии остается постоянным.

Уравнение баланса для средних значений поля. На практике представляют интерес не только мгновенные значения векторов поля, плотностей энергии, но и их среднее значение. Усреднение происходит за отрезок времени равный периоду гармонического колебания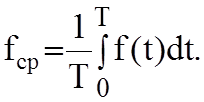 

При анализе используют метод комплексных амплитуд, который непосредственно применим в случае линейных уравнений. Обычная замена в формуле (3.2)  и комплексными векторами  и  приведет к неправильным результатам так, как ;  . Поэтому векторы представляют как:

;  ,

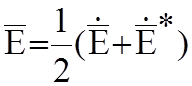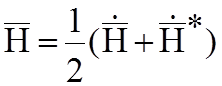где 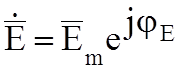; 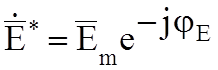- комплексно-сопряженная амплитуда.

Комплексный вектор Пойнтинга и среднее значение. Представляя вектор Пойнтинга таким образом и усредняя его за период времени, получим:

,

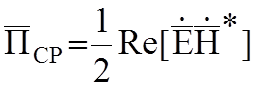где 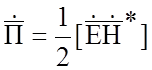-комплексный вектор Пойнтинга, а его вещественная часть есть среднее значение , который можно рассматривать как среднюю за период плотность потока энергии. Средний поток энергии через поверхность S, ограничивающая объем:

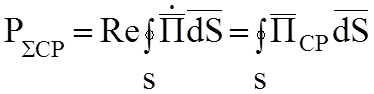
Аналогично вычисляются и другие интегралы. Выпишем окончательные результаты.

             Средняя мощность потерь :

                                      

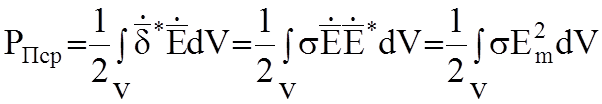
             Средняя мощность, выделяемая сторонними источниками в объем:

                                      

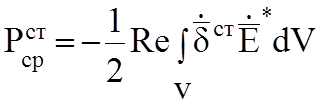
             Среднее значение электрической и магнитной энергии:

                                       ; 

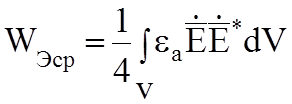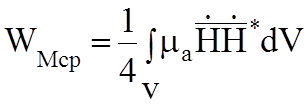
             Среднее значение плотностей электрической и магнитной энергии:

                                       ; 

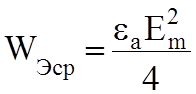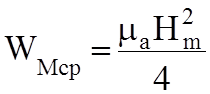
             Среднее за период изменение энергии равно нулю:

                                      

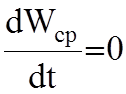
             Таким образом, усреднение по времени теоремы Умова-Пойнтинга (3.2) приводит к уравнению:

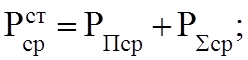
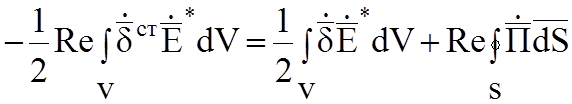    (3.3)

В среднем за период мощность сторонних источников расходуется на тепловые потери и на излучение из этого объема через поверхность S. Если , то поток энергии в среднем выходит из объема, если , то энергия поступает в объем из окружающего пространства.

В электродинамике рассматривают также комплексную мощность сторонних источников:

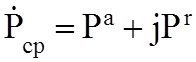                                                                   (3.4)

             Вещественная часть, или активная мощность равна средней за период мощности. Реактивная мощность  изменяется со временем по гармоническому закону с частотой 2w. Это означает, что в течение периода половину времени мощность имеет положительное значение, а вторую половину – отрицательное. Среднее за период , то есть реактивная энергия не расходуется.

             Резонансные явления из уравнения баланса комплексной мощности. Выделим мнимую часть, получим уравнение баланса реактивной мощности:

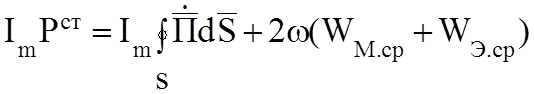                                                          (3.5)

             Предположим, что объем V представляет изолированную систему. Тогда реактивный и активный потоки энергии через поверхность S равны нулю и уравнения (3.4) и (3.3) примут вид:

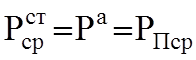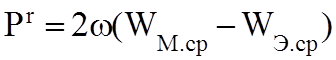                                       ;                  (3.6)

             В этом случае энергия электрического поля будет преобразовываться в магнитную и обратно, если , то этот процесс будет протекать без участия сторонних источников. Реактивная мощность сторонних источников  , а  мощность источника будет чисто активной. Это явление называют резонансом, его условие .

             Отношение:

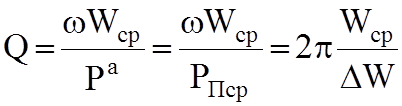                                                                            (3.7)

называют добротностью изолированной системы,

             где ;  - изменение энергии системы за период. Таким образом, добротность есть отношение запаса энергии W_ср и энергии расходуемой за период Т, умноженной на 2p.

             Скорость движения энергии равна:

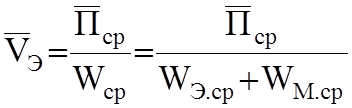                                             (3.8)