Закон
электромагнитной индукции Фарадея. Если замкнутый проводящий
контур ℓ поместить в переменное магнитное поле ![]() , то в
контуре возникает ток проводимости за счет наведенной в контуре электродвижущей
силы Є, величина которой определяется скоростью изменения магнитного потока.
Математически это записывается следующим образом,
, то в
контуре возникает ток проводимости за счет наведенной в контуре электродвижущей
силы Є, величина которой определяется скоростью изменения магнитного потока.
Математически это записывается следующим образом,

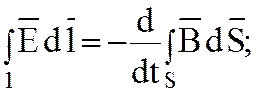 (1.15)
(1.15)
ЭДС в
контуре выражается через вектор напряженности электрического поля e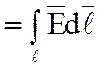 .
Физический смысл этого явления следующий: первоначально в проводящем контуре
токи отсутствуют, электроны неподвижны и на них магнитное поле
.
Физический смысл этого явления следующий: первоначально в проводящем контуре
токи отсутствуют, электроны неподвижны и на них магнитное поле ![]() не действует. Привести электроны в
движение, то есть, создать электрический ток может только электрическое поле
не действует. Привести электроны в
движение, то есть, создать электрический ток может только электрическое поле ![]() , которое и создается в контуре магнитным
полем
, которое и создается в контуре магнитным
полем ![]() . Таким образом, магнитное поле создает
электрическое, которое и создает электрический ток проводимости в контуре.
Справедливо и обратное заключение – имеющиеся токи создают магнитное поле.
Количественная связь между токами и созданными ими магнитными полями выражается
следующим законом, для вакуума
. Таким образом, магнитное поле создает
электрическое, которое и создает электрический ток проводимости в контуре.
Справедливо и обратное заключение – имеющиеся токи создают магнитное поле.
Количественная связь между токами и созданными ими магнитными полями выражается
следующим законом, для вакуума
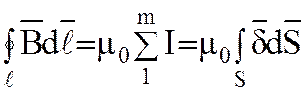 ,
(1.16)
,
(1.16)
где ![]() – алгебраическая сумма токов,
пронизывающих контур ℓ;
– алгебраическая сумма токов,
пронизывающих контур ℓ;
μ0=4π·10–7 Гн/м – постоянная в система СИ;
![]() – плотность тока, А/м2.
– плотность тока, А/м2.
Токи, составляющие
правовинтовую систему с направлением обхода контура, считаются положительными и
входят в сумму со знаком «+», левовинтовую систему – со знаком «–»; ток I5 в сумме дает ноль, I6
– не входит в сумму (рисунок 1.2). Внутри любого вещества существуют замкнутые
электронные токи (орбитальные, спиновые движения электронов), которые создают
магнитное поле. Эти токи характеризуются магнитным моментом ![]() (рисунок 1.3). При воздействии на вещество
внешнего магнитного поля в ориентировке магнитных моментов
(рисунок 1.3). При воздействии на вещество
внешнего магнитного поля в ориентировке магнитных моментов ![]() появляется упорядоченность, вещество
намагничивается, суммарный магнитный момент вещества будет отличен от нуля.
появляется упорядоченность, вещество
намагничивается, суммарный магнитный момент вещества будет отличен от нуля.
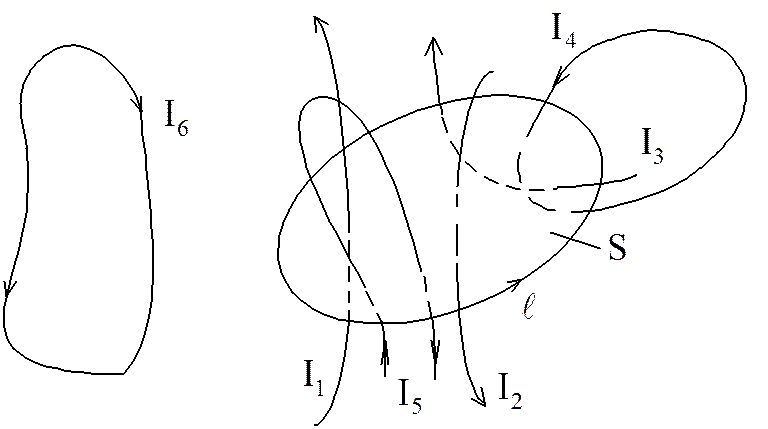
Рисунок 1.2

Намагниченность вещества характеризуют вектором намагниченности
![]() =
=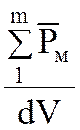 ;
; ![]() ,
(1.17)
,
(1.17)
где 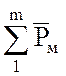 – геометрическая сумма магнитных моментов
элементарных токов в малом объеме dV.
– геометрическая сумма магнитных моментов
элементарных токов в малом объеме dV.
Влияние магнитных полей элементарных токов нужно учесть в формуле (1.16):
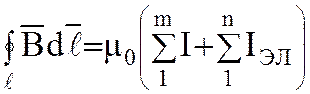 ,
(1.18)
,
(1.18)
где 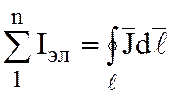 – алгебраическая сумма
элементарных токов, можно выразить через вектор намагниченности. Тогда
– алгебраическая сумма
элементарных токов, можно выразить через вектор намагниченности. Тогда
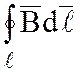
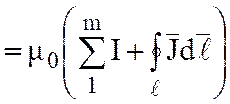 ;
;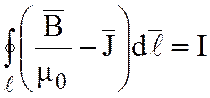 ;
;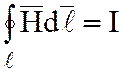 , (1.19)
, (1.19)
где 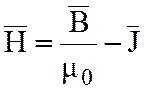 ;
; ![]() – напряженность магнитного поля.
– напряженность магнитного поля.
Магнитная проницаемость среды. Для линейных изотропных сред вектор ![]() пропорционален вектору
пропорционален вектору ![]() :
:
![]() =
=![]() ,
,
где ![]() – коэффициент магнитной
восприимчивости.
– коэффициент магнитной
восприимчивости.
Подставим в уравнение, тогда 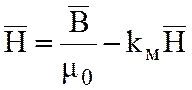 или
или
![]() ,
(1.20)
,
(1.20)
где ![]() , Гн/м – абсолютная
магнитная проницаемость среды. Для вакуума
, Гн/м – абсолютная
магнитная проницаемость среды. Для вакуума ![]() =0 и
=0 и ![]() , то есть магнитная проницаемость вакуума
равна
, то есть магнитная проницаемость вакуума
равна ![]() . Для среды вводится еще относительная
магнитная проницаемость
. Для среды вводится еще относительная
магнитная проницаемость
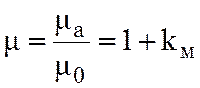 ,
,
безразмерная величина, ее указывают в справочнике. По магнитной восприимчивости среды делят на три группы:
- диамагнетики, μ<1 (вода, медь, серебро, ртуть …);
- парамагнетики, μ>1 (кислород, алюминий, платина…);
- ферромагнетики, μ>>1 (железо, кобальт, никель и их сплавы). Это нелинейные среды, имеется остаточная намагниченность.
Рассмотрим плотность тока смещения в веществе с параметрами εа; σ; μа.
Выделим объем V в вакууме, где отсутствуют электрические заряды и
токи (Q=0; ρ=0; ![]() =0). Запишем
рассмотренные уравнения для такого объема:
=0). Запишем
рассмотренные уравнения для такого объема:
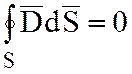 ;
; 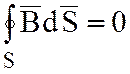
Эти уравнения идентичны, подтверждают принцип симметрии между электрическим и магнитным полем.
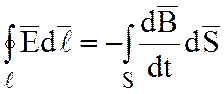 ;
; 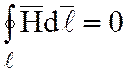
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.