Электромагнитные поля и волны. Основные понятия электродинамики, страница 3

На токе смещения базируется радиосвязь, а на токе проводимости проводная электросвязь,  использующая линии передачи.

Распространяющаяся в среде ЭМВ, несущая информацию, испытывает влияние среды. На создание и поддержание токов в среде тратится энергия ЭМВ, то есть амплитуда ЭМВ уменьшается по закону Е=Е_m·exp(–αz), где α – коэффициент затухания. Это тепловые потери в среде за счет наличия тока проводимости. За счет тока смещения в среде возникают поляризационные потери.

Рассмотрим поляризацию среды в электрическом поле. Это сложное явление. Грубая модель следующая. В среде есть молекулы полярные и неполярные, то есть электрически нейтральные.

В полярных молекулах центры тяжести суммарного отрицательного заряда и положительного не совпадают, и ее можно представить в виде электрического диполя с моментом (рисунок 1.1)

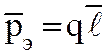                                                                                (1.6)

Такая полярная молекула во внешнем электрическом поле вектора  будет ориентироваться по полю, то есть  совпадет с .

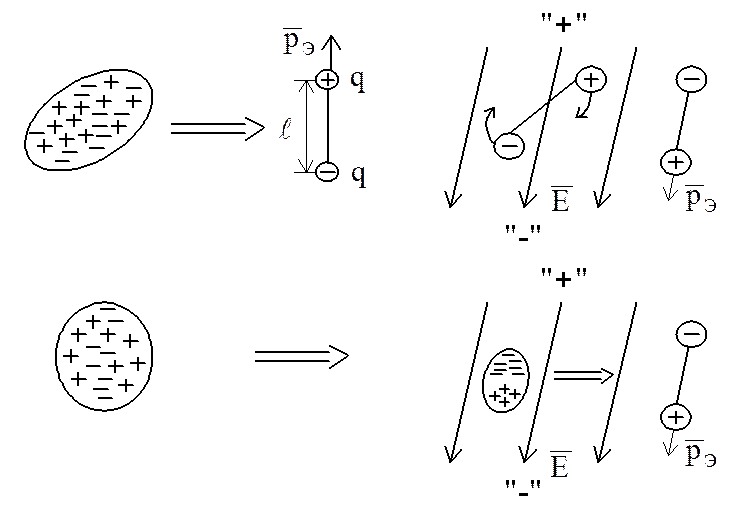
Рисунок 1.1

Неполярная молекула под действием электрического поля растянется, можно будет выделить положительный полюс и отрицательный. Эквивалентный ей диполь создается сориентированным  по полю. Упорядоченно ориентированные диполи в среде создают свое внутреннее электрическое поле, которое, суммируясь с внешним полем, изменяет его. При изменяющемся во времени электрическом поле =_mcos(ωt–φ), вектор  дважды за период изменяет направление и, соответственно, изменяют ориентацию диполи, ориентируясь по полю. На это тратится энергия ЭМВ, это будут поляризационные потери.

Суммарное электрическое поле в среде  за счет поляризации изменяется, и это надо учесть в законах. Для этого вводится вектор поляризованности

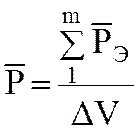,                                                                    (1.7)

Это есть векторная сумма дипольных моментов молекул в единице объема. Вектор поляризованности  суммируется с внешним полем  и их сумма есть вектор электрического смещения:

,                                                                        (1.8)

где ε₀=8,86·10^–12 Ф/м, константа в системе СИ.

В линейных, изотропных, однородных средах вектор поляризованности пропорционален вектору

,                                                                         (1.9)

где  – коэффициент диэлектрической восприимчивости.

Отсюда

=,                       (1.10)

где ε_а= – абсолютная диэлектрическая проницаемость среды, Ф/м; ее можно записать так

,

где ε=– относительная диэлектрическая проницаемость, =.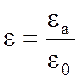

Таким образом, в электрическом поле имеется три вектора , , . Зная ε_а и один из векторов, можно рассчитать остальные два. В электродинамике оставили вектор .

Рассмотрим характеристики магнитного поля.

Магнитное поле оказывает силовое воздействие на движущиеся электрические заряды, на проводники с током. Эта сила пропорциональна величине заряда и скорости его движения, а также величине магнитного поля, которую назвали магнитной индукцией и обозначили , имеет размерность Вб/м² или Тесла. Направление действия силы определяется векторным произведением  по правилу правого винта:

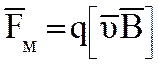,                                                                     (1.11)

где q – заряд, единичный, положительный;

       – вектор скорости заряда;

       – вектор магнитной индукции.

Произведение модуля вектора  на поверхность S, через которую проходят силовые линии вектора , называют магнитным потоком Ф_м. В общем случае

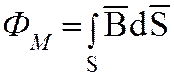,                                                                   (1.12)

где d – вектор-площадка, равный

=,                                                                       (1.13)

где  – орт-вектор нормали к площадке dS.

Магнитный поток через замкнутую поверхность всегда равен нулю:

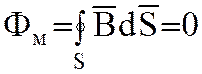                                                               (1.14)

Это значит, что силовые линии магнитного поля всегда замкнуты сами на себя и в природе, таким образом, отсутствуют магнитные заряды, аналогичные электрическим.