Расчет по областям применения математических моделей теории телетрафика (коммутационные системы, потоки вызовов, характеристики качества обслуживания, время обслуживания), страница 4

Для нахождения  воспользуемся формулой:

С помощью полученных значений найдём :

По данным   и Р найдём в приложении 4(1) значение коэффициентов  и . Для данного блока =1.62, =3.6.

Ёмкость пучка равна:

V=1.62∙20+3.6=36

2.  Аналогично определим ёмкость пучка для блока 80х120х400 со структурными параметрами:

, , .

По ранее использованным формулам рассчитаем интенсивность нагрузки, обслуженной m промежуточными линиями:

=1.62∙13.3=6.1318 Эрланг.

Число выходов:

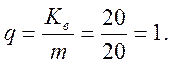
Определим значение доступности :

По известным значениям Р= 0.005 и =13 с помощью приложения 4(1) найдём значение коэффициентов  и . Для данного блока =1.5, =4.2.

Ёмкость пучка равна:

V=1.5∙20+4.2=35

Вывод:

Из расчётов видно, что при одинаковой величине нагрузки ёмкость пучка для блоков 60х80х400  и 80х120х400 различна.

Экономически выгодней использовать блок 80х120х400, так как здесь используется меньшее число линий (на одну), чем в блоке  60х80х400.

Задача 7

Условие:

На выходе ступени БСЛ АТСКЭ поступает по двум пучкам линий, математическое ожидание которой У1=26 эрланг У2=24. На выходе ступени объединённая нагрузка распределяется по направлениям пропорционально коэффициентам Кi (К1, К2, К3): К1=0.12, К2=0.34, К3=0.54.

Определить расчётное значение нагрузки каждого направления и относительное отклонение расчётного значения нагрузки от её математического ожидания. По результатам сделать вывод.

Решение:

В различные дни недели, месяцы, года в ЧНН нагрузка изменяется постоянно, и это изменение приводит к  изменению качественных показателей качественного обслуживания - они ухудшаются. Чтобы качественные показатели качества обслуживания не превышали заданных значений, необходимо использовать такую нагрузку, при которой с max вероятностью качественные показатели остаются постоянными, такой нагрузкой является расчётная нагрузка, поэтому при объединении и разделении потоков нагрузки на различных ступенях искания различных сетей величины расчётных нагрузок должны определятся в следующей последовательности: в случае объединения потоков нагрузки необходимо найти математическое ожидание суммарной нагрузки, затем перейти к расчётному значению нагрузки для определения числа устройств, обслуживающих суммарную нагрузку.

где У =

При разделении нагрузок по направлениям, следует определить математическое ожидание нагрузки данного направления из расчетной нагрузки:

                

Необходимо найти расчетное число нагрузок, по отношению к которым определяется число соединительных линий или коммутационных устройств:

               У=У₁+У₂ = Эрланг.

Определим число коммутационных устройств:

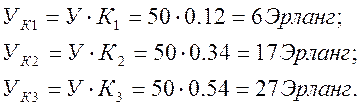
Определим расчётную нагрузку для  каждого У_i:

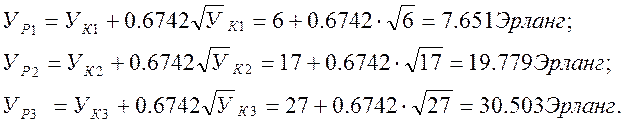
Определим математические ожидания нагрузки данного направления из расчётной нагрузки:

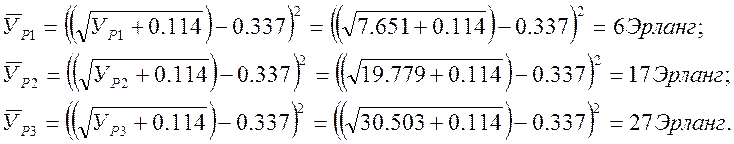
Найдем математическое отклонение:

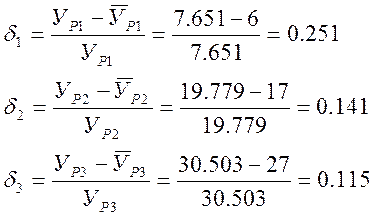
Вывод:

С увеличением нагрузки, величина относительного отклонения более стабильна и соответственно влияния на качественные характеристики коммутационной системы будут менее заметны, в отличие от систем с малыми нагрузками.

Заключение

В курсовом проекте был проведён ряд вычислений по некоторым областям применения математических моделей теории телетрафика (коммутационные системы, потоки вызовов, характеристики качества обслуживания, время обслуживания) и сделаны выводы по выполненным расчетам.

В первой задаче ставилась цель закрепления материала по изучению математических моделей простейшего и примитивного потоков вызовов. Получив графическую зависимость вероятности поступления  вызовов от числа источников, можно сделать вывод, что с увеличением числа вызовов вероятности поступления уменьшаются и стремятся друг к другу. На промежутке от 2 до 5 вызовов вероятность примитивного потока больше чем у простейшего.