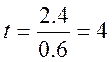
Вероятность
ожидания свыше допустимого времени ![]() равна:
равна:
Р(γ>t)=f(![]() ,t)=0.001
,t)=0.001
Задача 5
Условие:
Неполнодоступный пучок линий в однозвенной системе с отказами обслуживает нагрузку У=25 эрланг при доступности d=15.
Определить ёмкость пучка U при двух значениях потерь Р1=3‰ и Р2=10‰. Сравнить полученные результаты. Рассчитать структурные параметры и построить неполнодоступную однозвенную систему.
Решение:
Для решения данной задачи воспользуемся методом О’Делла. В данном методе ёмкость пучка определяется :
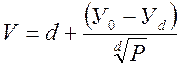 ,
,
но при фиксированных значениях d и P формула приобретает вид линейной зависимости числа соединительных устройств от интенсивности нагрузки:
![]() ,
,
где ![]() и
и ![]() -
коэффициенты, определяемые по приложению 4(1).
-
коэффициенты, определяемые по приложению 4(1).
Для Р1=0.003
и d=15 получим значения ![]() =1.47 и
=1.47 и ![]() =4.9.
=4.9.
С помощью этих коэффициентов можно определить V1:
![]()
Аналогично по
приложению 4(1) определяем коэффициенты ![]() и
и ![]() для Р2=0.01 и d=15
– получается
для Р2=0.01 и d=15
– получается ![]() =1.36 и
=1.36 и ![]() =3.9.
=3.9.
Рассчитываем V2:
![]()
Сделаем расчёт и построим схемы включения для V1=42
Рассчитаем число нагрузочных групп g:
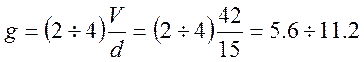
С экономической точки зрения целесообразней выбрать g=6.
Решив следующую систему уравнений, определим количество коммутаторов:
d=15=k1+ k2+ k3+ k6
V=42=6· k1+3· k2+2· k3+ k6
V-d=27=5· k1+2· k2+ k3.
k1=![]() =
=![]() =2.8.
=2.8.
Пусть k1=2, тогда:
17=2· k2+ k3.
Примем k2=8 ![]() k3=1
и k6=4.
k3=1
и k6=4.
Схема ступенчатого включения для данных параметров и матрица связности представлены на рисунке 5.1. Все приведённые ниже схемы считаются составленными правильно, так как выполняются условия оптимальности матрицы: разница между значениями матрицы и между значениями столбца, указывающего общее число связей, по абсолютной величине не превышает единицы.
Сделаем расчёт
и построим схемы включения для ![]() =38.
=38.
Рассчитаем коэффициент уплотнения:
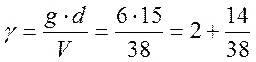
Отсюда число
линий V![]() , полученное
путём запараллеливания по r+1(по 3) точек коммутации,
составляет 14, а число линий, соответствующее запараллеливанию по r (по 2)составляет:
, полученное
путём запараллеливания по r+1(по 3) точек коммутации,
составляет 14, а число линий, соответствующее запараллеливанию по r (по 2)составляет:
![]() =38-14=24
=38-14=24
Определяем число шаговых цилиндров:
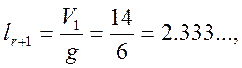
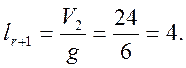
Схема включения со сдвигом и матрица связности для данных параметров приведены на рисунке 5.2.
Вывод:
В неполнодоступной схеме со ступенчатым включением число соединений точек коммутации отдельных нагрузочных групп больше чем в равномерной неполнодоступной схеме цилиндров.
При увеличении потерь ёмкость пучка уменьшается, а это приводит к более эффективному использованию соединительных линий.

Задача 6
Условие:
Нагрузка, поступающая на ступень ГИ АТСК, обслуживается в данном направлении пучком линий с доступностью Кbq=20 при потерях Р= 0.005. Нагрузка на один вход ступени а=0.46 эрланг, нагрузка в направлении У=20 эрланг.
Определить методом эффективной доступности ёмкость пучка U при установке на ступени блоков 60*80*400 и 80*120*400. Сравнить полученные результаты.
Решение:
Для решения данной задачи будем использовать метод эффективной доступности.
1. Определим ёмкость пучка при установке на ступени блока 60х80х400.
Структурные параметры данного блока таковы:
![]() .
.
Для нахождения ёмкости пучка воспользуемся формулой:
![]()
Коэффициенты ![]() и
и ![]() находятся
из таблицы значений в приложении 4(3). Для этого необходимо знать значение
вероятности потерь и эффективной доступности пучка.
находятся
из таблицы значений в приложении 4(3). Для этого необходимо знать значение
вероятности потерь и эффективной доступности пучка.
Эффективной доступности пучка вычисляется по формуле:
![]()
где ![]() - коэффициент, определяемый зависимостью
потерь от доступности и распределением вероятностей доступности. В данной
задаче принимаем
- коэффициент, определяемый зависимостью
потерь от доступности и распределением вероятностей доступности. В данной
задаче принимаем ![]() =0.7.
=0.7.
Математическое ожидание доступности определяется:
![]()
где ![]() - интенсивность нагрузки, обслуженной m промежуточными линиями. Определяется по формуле:
- интенсивность нагрузки, обслуженной m промежуточными линиями. Определяется по формуле:
![]()
![]() =0.46∙15=6.9 Эрланг.
=0.46∙15=6.9 Эрланг.
![]()
Найдём число выходов с коммутатора q:
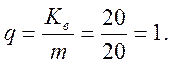
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.