Расчет по областям применения математических моделей теории телетрафика (коммутационные системы, потоки вызовов, характеристики качества обслуживания, время обслуживания)

Техническое задание

Задача 1. На коммутационную станцию поступает поток вызовов, создающий нагрузку У=2.8 эрланг. Определить вероятность поступления ровно i вызовов Pi (i = 0, 1, 2, 3…, n) при примитивном потоке от 7^ми источников и Pi (i = 0, 1, 2, 3…,j) при простейшем потоке вызовов. Построить кривые распределения вероятностей Pi = f(i) и произвести сравнение полученных результатов.

Задача 2. В блок абонентского искания(БАИ) цифровой системы коммутации типа ДХ – 200 включено 3904 абонентских линий.

Определить поступающую на БАИ нагрузку, если среднее число вызовов от одного абонента С=2.8 выз./ч., среднее время разговора Т=120 с.,  доля вызовов закончившихся разговором Рр=0.6. Нумерация на сети шестизначная.  

Задача 3. Полнодоступный пучок из V=7  каналов обслуживает поток вызовов, поступающий от источников нагрузки, включенных в концентратор цифровой системы коммутации.

Определить пропускную способность пучка, т.е. нагрузку У, которая может поступать на этот пучок при заданной величине потерь по вызовам Рв=4‰ в случае простейшего потока и примитивного потока от N1=40 и N2=20 источников. По результатам расчётов сделать выводы.

Задача 4. На коммутационный блок координационной станции типа АТСК поступает простейший поток вызовов, который создаёт нагрузку Уб=36 эрланг при средней длительности занятия входа блока t_б =72 с. Блок обслуживается одним маркёром, работающим в режиме с условными потерями при постоянной длительности занятия t_м=0.6 с. Задержанные вызовы обслуживаются в случайном порядке независимо от очерёдности их поступления.

Определить вероятность ожидания свыше допустимого времени t_д=2.4 с и среднее время ожидания задержанных вызовов t_з.      

Задача 5. Неполнодоступный пучок линий в однозвенной системе с отказами обслуживает нагрузку У=25 эрланг при доступности d=15.

Определить ёмкость  пучка U при двух значениях потерь Р1=3‰ и Р2=10‰. Сравнить полученные результаты. Рассчитать структурные параметры и построить неполнодоступную однозвенную систему.

Задача 6. Нагрузка, поступающая на ступень ГИ АТСК, обслуживается в данном направлении пучком линий с доступностью Кbq=20 при потерях Р= 0.005. Нагрузка на один вход ступени  а=0.46 эрланг, нагрузка в направлении У=20 Эрланг.

Определить методом эффективной доступности ёмкость пучка U при установке на ступени блоков 60*80*400 и 80*120*400. Сравнить полученные результаты.

Задача 7. На выходе ступени БСЛ АТСКЭ поступает по двум пучкам линий, математическое ожидание которой У1=26 Эрланг У2=24. На выходе ступени объединённая нагрузка распределяется по направлениям пропорционально коэффициентам Кi (К1, К2, К3): К1=0.12, К2=0.34, К3=0.54.

Определить расчётное значение нагрузки каждого направления и относительное отклонение расчётного значения нагрузки от её математического ожидания. По результатам сделать вывод.

Задача 1

Условие:

На коммутационную станцию поступает поток вызовов, создающий нагрузку У=2.8 эрланг. Определить вероятность поступления ровно i вызовов Pi (i = 0, 1, 2, 3…, n) при примитивном потоке от 7^ми источников и Pi (i = 0, 1, 2, 3…,j) при простейшем потоке вызовов. Построить кривые распределения вероятностей Pi = f(i) и произвести сравнение полученных результатов.

Решение:

Рассчитаем вероятность поступления семи вызовов для примитивного потока.

Примитивным потоком называется ординарный поток параметр, которого, прямопропорционален числу свободных источников в состоянии обслуживающей системы.

 

где  - параметр примитивного потока;

- число источников;

- число занятых источников;

- параметр потока вызовов от одного свободного источника, .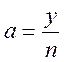

Вероятностный процесс поступления вызовов примитивного потока описывается формулой распределения Бернулли:

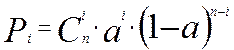
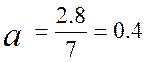Эрланг

Рассчитаем число сочетаний:

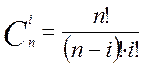
Определим вероятность отсутствия вызовов:

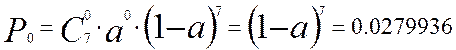
Для определения вероятности поступления одного, двух и более – до семи вызовов воспользуемся рекуррентной формулой:

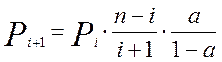
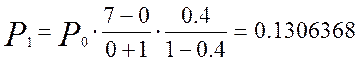
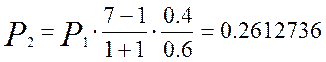
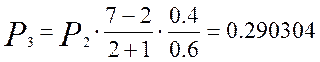
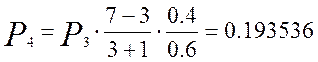
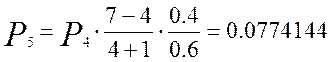
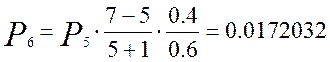
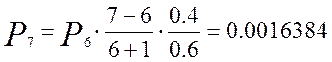
Кривая распределения вероятностей от числа поступающих вызовов для примитивного потока изображена на рисунке 1.

Рассчитаем вероятность поступления семи вызовов для простейшего потока.

Простейшим потоком вызовов называется стационарный ординарный поток без последействия.

Вероятностный процесс поступления вызовов простейшего потока определяется законом распределения Пуассона:

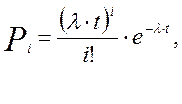
где λ·t – количество вызывающих абонентов в заданном моменте времени.

λ·t=У

Простейший поток задаётся семейством вероятностей поступления числа вызовов в определённый момент времени.

Рассчитаем вероятность отсутствия вызова:

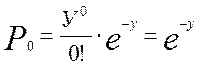
Для определения вероятности поступления одного и более вызовов простейшего потока используем рекуррентную формулу:

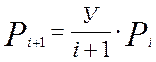
Вероятность поступления одного вызова равна:

 

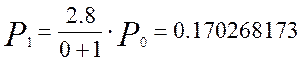
Аналогично определим вероятность для следующих шести вызовов:

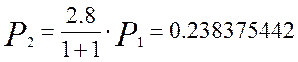
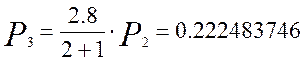
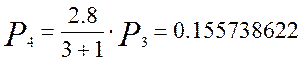
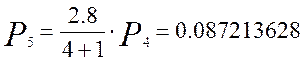
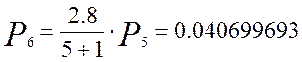
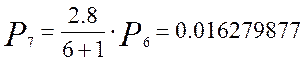
Кривая распределения вероятностей от числа поступающих вызовов для простейшего потока показана на рисунке 1.

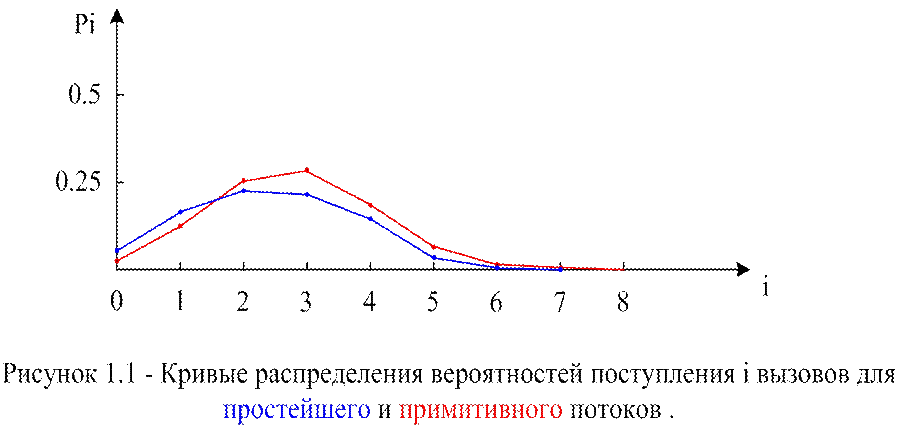
Из графиков видно, что с увеличением числа вызовов вероятности поступления уменьшаются и стремятся друг к другу. На промежутке от 2 до 5 вызовов вероятность примитивного потока больше чем у простейшего.