Другие предметы \ Теория телетрафика

Расчет по областям применения математических моделей теории телетрафика (коммутационные системы, потоки вызовов, характеристики качества обслуживания, время обслуживания), страница 2

Задача 2

Условие:

В блок абонентского искания(БАИ) цифровой системы коммутации типа ДХ–200 включено 3904 абонентских линий.

Определить поступающую на БАИ нагрузку, если среднее число вызовов от одного абонента С=2.8 выз./ч., среднее время разговора Т=120 с.,  доля вызовов закончившихся разговором Рр=0.6. Нумерация на сети шестизначная. 

Решение:

Так как по условию задачи из всех возможных исходов, которыми закончится поступивший вызов, задана только доля состоявшихся разговоров Рр, то расчёт нагрузки следует вести по формуле, в которой остальные исходы вызовов учитываются коэффициентом α, который определяется по графику на странице 52(2).

Среднюю длительность разговора можно определить по формуле:

 

где  - среднее время ответа станции, 3с;

 - среднее время набора номера, которое определяется для декадного набора и частотного отдельно:

=1.5·m – для декадного набора;

=0.8·m – для частотного набора,

где m – число знаков абонентского номера;

 - среднее время установления соединения, 0с;

 - среднее время посылки вызова, 7с;

 - среднее время отбоя, 0с

Пусть 50% абонентов используют декадный набор номера и остальные 50% - частотный.

Тогда для ДН:

=3+1.5·6+0+7+120+0=139с.

Для ЧН:

=3+0.8·6+0+7+120+0=134.8с.

По графику 2.3(2) определяем значение α:

при Т=120 с и Рр=0.6 α=1.1

Рассчитаем нагрузку от абонентов с ДН и ЧН:

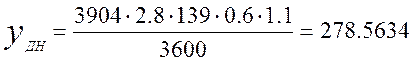
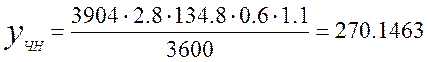
Общую нагрузку поступающую на БАИ определим как сумму  и :

=+=278.5634+270.1463=548.7097 Эрланг

Задача 3

Условие:

Полнодоступный пучок из V=7 каналов обслуживает поток вызовов, поступающий от источников нагрузки, включенных в концентратор цифровой системы коммутации.

Определить пропускную способность пучка, т.е. нагрузку У, которая может поступать на этот пучок при заданной величине потерь по вызовам Рв=4‰ в случае простейшего потока и примитивного потока от N1=40 и N2=20 источников. По результатам расчётов сделать выводы.

Решение:

Обслуживание полнодоступным пучком простейшего потока описывается первой формулой Эрланга:

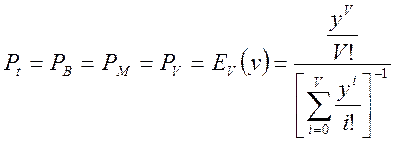
По причине сложности расчёта воспользуемся таблицей (приложение 3(2)):

При Рв=4‰ и V=7      У=2.053 Эрланг

Обслуживание полнодоступным пучком примитивного потока описывается формулой Энгсета:

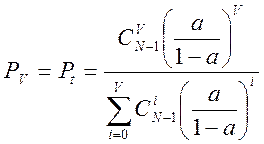
По причине сложности расчёта воспользуемся таблицей (приложение 4(2)):

При Рв=4‰, V=7, N=40      У=2.21 Эрланг

При Рв=4‰, V=7, N=20      У=2.403 Эрланг

По результатам решения можно сделать вывод, что при увеличении числа источников в примитивном потоке нагрузка уменьшается.

Задача 4

Условие:

На коммутационный блок координационной станции типа АТСК поступает простейший поток вызовов, который создаёт нагрузку Уб=36 эрланг при средней длительности занятия входа блока tб =72 с. Блок обслуживается одним маркёром, работающим в режиме с условными потерями при постоянной длительности занятия tм=0.6 с. Задержанные вызовы обслуживаются в случайном порядке независимо от очерёдности их поступления.

Определить вероятность ожидания свыше допустимого времени tд=2.4 с и среднее время ожидания задержанных вызовов tз.     

Решение:

С помощью формул Берка были построены кривые (рисунок 1и рисунок 2 приложения 3(1)). Эти кривые дают возможность определить значения требуемых величин: вероятность  ожидания свыше допустимого времени Р(γ>t) и среднее время ожидания задержанных вызовов .

определяется по кривой рисунка 2 приложения3(1) в зависимости от нагрузки на маркёр:

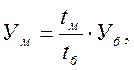
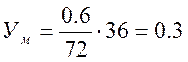Эрланг.

=0.75

Вычислим среднее время ожидания задержанных вызовов:

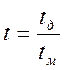 - время, измеренное в единицах длительности занятия.

С помощью этого параметра и нагрузки на маркёр по графику рисунка 1 приложения 3(1) определяется вероятность  ожидания свыше допустимого времени.

Скачать файл