Передача коротких сообщений (SMS) в системах мобильной связи, страница 5

	Показатели	Метод 1	Метод 2	Метод 3	Метод 4
1	Вероятность успешного вызова	-	0,833	0,774	0,774
2	Вероятность успешной доставки	0,77	0,883	0,8829	0,986
3	Надежность (достоверность)	0,77	0,736	0,683	0,763
4	Нормированная надежность	0,906	0,866	0,804	0,898
5	Затраты на вызов	-	70,01	47,32	47,32
6	Затраты на доставку	2768	6,70	6,70	27,566
7	Полные затраты	2768	76,71	52,51	68,66
8	Задержка на вызов	-	3,3	1,96	1,96
9	Задержка на доставку	2,747	1,62	1,62	4,559
10	Полная задержка	2,747	4,92	3,58	6,519

Вывод

В таблицах 3.2 и 3.3 нормализованная надежность доставки - надежность доставки поделенная на Рup. Это вероятность успешной доставки сооб­щения, если источник питания МС включен. Эта величина представляет интерес, так как если источник питания выключен, то никакие ухищре­ния не обеспечат успешную доставку короткого сообщения.

  Как видно из таблицы 3.2 и 3.3 метод 1 обеспечивает максимальную на­дёжность при минимальной задержке. Это достигается за счет прямой доставки КС в каждую из сот, в которой может оказаться нужная нам мобильная станция. Однако затраты на доставку в этом случае достаточ­но велики, что для нормально загруженного прямого контрольного кана­ла может оказаться недопустимым. Метод 3 характеризуется минималь­ными затратами. Если затраты играют основную роль, то этот метод ока­зывается наиболее приемлемым. Однако этот метод характеризуется ми­нимальной надёжностью. Надёжность для четвертого метода незначи­тельно отличается от надежности, обеспечиваемой первым методом, затраты для него существенно меньше, чем для первого. Это может стать определяющим фактором при условии, что выбор метода должен осно­вываться на таких показателях, как затраты и надежность. Задержка для последних двух методов примерно одинакова и, если показатели задерж­ки не играют

существенной роли, этот фактор может не приниматься разработчиком во внимание. 

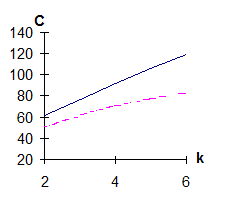
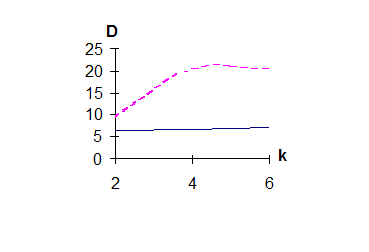
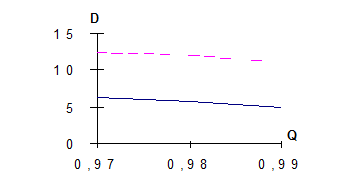
Рисунок 3.2. Графики зависимости показателей, Р,С, D от допустимого числа повторений

 

Рисунок 3.3.  Графики зависимости показателей, Р, С, D от качества канала

  На рис. 3.2. приведены графики зависимости показателей Р, С, D от допустимого числа повторении для независимых и группирующихся ошибок. Расчеты приведены для k=l=2.

  Анализируя графики (рисунок 3.2.), можно сделать следующие выво­ды. С ростом k= l надежность доставки КС растет, средние затраты так­же растут. Причем затраты при группировании ошибок больше, чем при независимых. Это объясняется тем, что при расчете стоимости для независимых ошибок учитывается только качество канала, при группирующихся ошибках необходимо так же принимать во внимание состояние МС. По задержке наилучшие результаты в случае группирующихся ошибок.

  Данные результаты говорят о том, что методы доставки КС эффективны как при группирующихся ошибках, так и при независимых, не смотря на то, что в каналах с группированием ошибок  условия передачи  хуже.

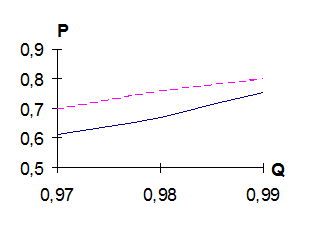
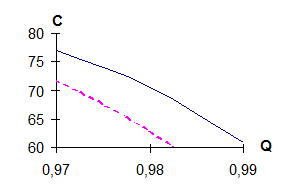
  Если загрузка прямого канала не очень велика, то можно пой­ти на увеличение числа повторений. Графики, приведенные на рис. 3.3. для четвертого метода, позволяют дать оценку параметров Р, С и D в зависимости от качества канала.