Передача коротких сообщений (SMS) в системах мобильной связи, страница 4

   Кроме того, будем считать, что общее время доставки КС достаточно мало и состояние МС не изменится за это время. Будем также считать состояние станции «хорошим» если она принимает переданный ей сигнал без замирания и «плохим» - в противном случае. В «хорошем» состоянии МС находится с вероятностью1-Ре, а в «плохом» - с вероятностью Ре. С целью сокращения записей примем

 

где состояния канала 1 и 2, cooтветственно, хорошее и плохое. Тогда матрица переходов из одного состояния в другое запишется в виде: 

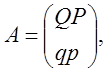                                                                                                          (3.19)

 

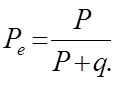где  P+Q=l,  p+q=1,

Метод 1.

Для модели Гильберта запишем вероятность успешной доставки в виде:                                                                                           

(3.20)

Затраты на одну доставку - bN слов, поэтому средние затраты:

(3.21)

здесь второе слагаемое - затраты на неудачную доставку КС.

Среднее время успешной доставки КС:

(3.22)

Так как

 Метод 2.

Вероятность успешного вызова МС, нахо­дящейся в зоне, где она была зарегистрирована в последний раз, в ре­зультате k вызовов равна:

(3.23)

Вероятность успешной доставки КС зависит от состояния канала и определяется выражением:

(3.24)

Общая вероятность доставки КС:

 

Каждый вызов использует a слов для каждой из т сот в зоне, поэтому затраты на вызов:

(3.25)

Затраты на передачу КС: 

(3.26)

Передача сообщения состоится, если вызов был успешен, поэтому общие затраты равны:

Составляющая задержки, обусловленная вызовом:

(3.27)

Составляющая задержки, обусловленная передачей КС:

(3.28)

Среднее время задержки, при условии успешной доставки:

(3.29)

Метод 3.

Вероятность успешного вызова при условии, что число повторений не превышает (к-2), определяется в этом случае выражением:

(3.30)

Затраты на вызов состоят из трех составляющих: затрат на вызов со­ты, затрат на вызов зоны (число повторений(к-1) раз), затрат на неудач­ный вызов:

(3.31)

Задержка, обусловленная пейджингом:

(3.32)

Так как                                                  то

  Метод 4.

Вероятность успешной доставки определяется выражением:

(3.33)

Затраты на доставку КС:

(3.34)

Среднее время, затраченное на передачу:

(3.35)

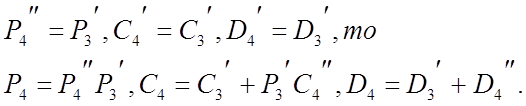Так как 

Результаты расчетов для k=2 и l=2 сведены в таблицу   3.3.

Таблица 3.3. Вероятность успешной доставки, затраты на доставку и задержка