





Электромагнитное поле, создаваемое переменными во
времени источниками ![]() , частично теряет с ним связь и
существует самостоятельно, не зависимо от источников. Это возможно, благодаря
способности электрического поля создавать магнитное и наоборот. Это переменное
электромагнитное поле, потерявшее связь с источником и есть электромагнитная
волна, распространяющаяся в окружающее пространство в радиальных направлениях
от источника. Процесс создания ускоренно движущимися зарядами (то есть
переменными во времени источниками) электромагнитных волн называют излучением.
В среде без потерь (s=0) величина векторов
, частично теряет с ним связь и
существует самостоятельно, не зависимо от источников. Это возможно, благодаря
способности электрического поля создавать магнитное и наоборот. Это переменное
электромагнитное поле, потерявшее связь с источником и есть электромагнитная
волна, распространяющаяся в окружающее пространство в радиальных направлениях
от источника. Процесс создания ускоренно движущимися зарядами (то есть
переменными во времени источниками) электромагнитных волн называют излучением.
В среде без потерь (s=0) величина векторов ![]() и
и ![]() излученных волн
излученных волн
изменяется
от расстояния как 1/R, то есть сравнительно медленно убывает, поэтому
оказывается возможной радиосвязь на значительные расстояния. Устройства
предназначенные для излучения ЭМВ называют антенной передающей. Для приема ЭМВ
используют приемные антенны. В электродинамике чаще решается прямая задача о
нахождении векторов поля по известным источникам. Плотность сторонних токов ![]() в источниках зависит от времени и
пространственных координат по сложным законам, которые в точности неизвестны
или известны приближенно. Самое простое решение получается когда
в источниках зависит от времени и
пространственных координат по сложным законам, которые в точности неизвестны
или известны приближенно. Самое простое решение получается когда ![]() =const, то есть не зависит от
пространственных координат. Смотрите формулы (5.10, 5.11). Это значит, что в
данный момент времени t амплитуда
=const, то есть не зависит от
пространственных координат. Смотрите формулы (5.10, 5.11). Это значит, что в
данный момент времени t амплитуда ![]() одинакова в любой точке
источника, то есть не зависит от
одинакова в любой точке
источника, то есть не зависит от ![]() .
Этого можно добиться, если размеры излучателя много меньше длины волны l. Такие излучатели называют элементарными. В электродинамике их три
вида:
.
Этого можно добиться, если размеры излучателя много меньше длины волны l. Такие излучатели называют элементарными. В электродинамике их три
вида:
- электрический элементарный излучатель
ЭЭИ (![]() );
);
- магнитный элементарный излучатель ЭМИ
(![]() );
);
- элемент Гюйгенса, элемент фронта
волны (![]() ), в пределах которого векторы
), в пределах которого векторы ![]() и
и ![]() постоянны
по амплитуде и фазе.
постоянны
по амплитуде и фазе.
Рассчитать ЭМП элементарных излучателей просто. Любой сложный излучатель можно представить как бесконечную сумму элементарных излучателей, а ЭМП сложного излучателя на основании принципа суперпозиции можно получить суммированием ЭМП элементарных излучателей с учетом их амплитуды и фаз в точке приема. Для этого и вводятся в рассмотрение элементарные излучатели.
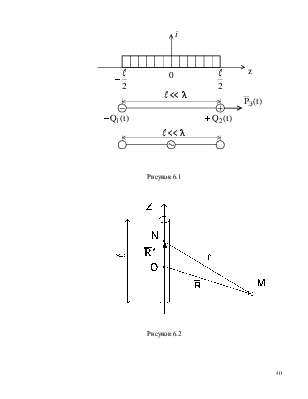
6.1 Элементарный электрический излучатель
Его
можно получить, взяв участок провода ![]() с переменным током
с переменным током ![]() очень малой длины
очень малой длины ![]() .
Тогда для какого-то момента времени t1 амплитуда тока и фаза его будет постоянна в любом
сечении, то есть не зависит от
.
Тогда для какого-то момента времени t1 амплитуда тока и фаза его будет постоянна в любом
сечении, то есть не зависит от ![]() (рисунок
6.1, 6.2). Пусть ось Z направлена вдоль оси ЭЭИ, который занимает интервал
(рисунок
6.1, 6.2). Пусть ось Z направлена вдоль оси ЭЭИ, который занимает интервал 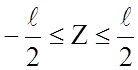 . Мгновенные значения тока излучателя от
координат Z не зависят, то есть:
. Мгновенные значения тока излучателя от
координат Z не зависят, то есть:
![]() , при
, при 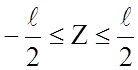
Используя закон сохранения заряда можно показать, что ЭЭИ эквивалентен электрическому диполю с гармонически изменяющимся во времени электрическим моментом:
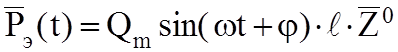
Заряды Q(t) сосредоточены на концах ЭЭИ, тогда ЭЭИ можно назвать электрическим диполем с переменными зарядами.
ЭЭИ
со строго неизменным по его длине током практически неосуществим, и
представляет удобную идеализированную излучающую систему для анализа более
сложных излучателей. Реальная антенна, близкая по своим свойствам к ЭЭИ,
представляет собой два тонких провода с металлическими шарами на концах, которые
имеют большую емкость, благодаря ![]() и шарам величина тока
мало изменяется вдоль длины
и шарам величина тока
мало изменяется вдоль длины ![]() . Такую излучающую
систему называют диполем Герца.
. Такую излучающую
систему называют диполем Герца.
6.2 Электромагнитное поле элементарного электрического излучателя
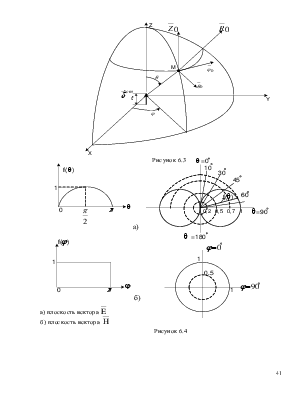
При
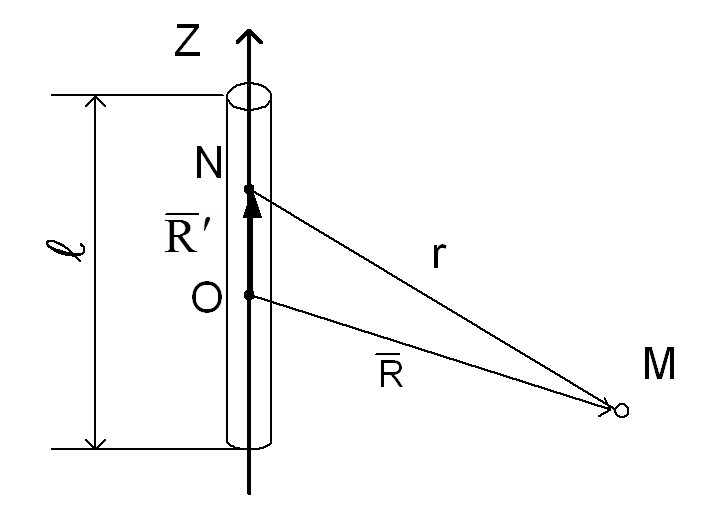
анализе ЭМП ограничимся точками наблюдения М, для которых выполняется условие ![]() , тогда
, тогда ![]() (рисунок
6.2). Применим формулу (5.11), в которой
(рисунок
6.2). Применим формулу (5.11), в которой 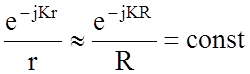 выносится
за знак интеграла. Интегрирование
выносится
за знак интеграла. Интегрирование ![]() по объему излучателя
представим так:
по объему излучателя
представим так:
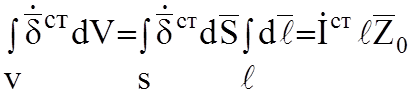
В итоге получаем:
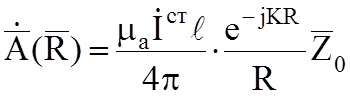
Перейдем и сферической системе координат (рисунок 6.3). Векторный потенциал
![]() в
сферической системе будет иметь в точке М две составляющие:
в
сферической системе будет иметь в точке М две составляющие:
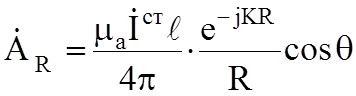 ,
, 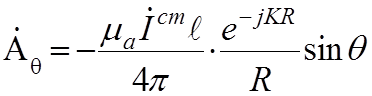
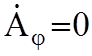
Зная все составляющие
вектора ![]() рассчитывают все составляющие векторов
рассчитывают все составляющие векторов ![]() и
и ![]() ,
используя (5.4, 5.5) или (2.9).
,
используя (5.4, 5.5) или (2.9).
В результате ЭМП ЭЭИ имеет вид:
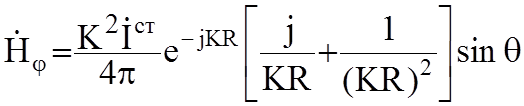 ;
;
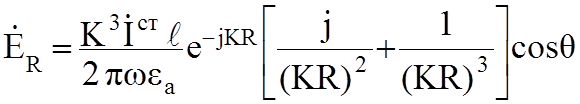 ; (6.1)
; (6.1)
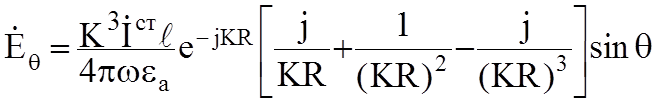
ЭМП
имеет одну составляющую вектора ![]() и две вектора
и две вектора ![]() , ЭМП не зависит от азимутального угла j, что является следствием осевой симметрии излучателя. Зависимость
векторов поля от расстояния R позволяет выделить вокруг излучателя три зоны:
ближнюю (
, ЭМП не зависит от азимутального угла j, что является следствием осевой симметрии излучателя. Зависимость
векторов поля от расстояния R позволяет выделить вокруг излучателя три зоны:
ближнюю (![]() ), промежуточную (
), промежуточную (![]() )
и дальнюю (
)
и дальнюю (![]() ). В промежуточной зоне все слагаемые в
(6.1) имеют один порядок и должны учитываться все.
). В промежуточной зоне все слагаемые в
(6.1) имеют один порядок и должны учитываться все.
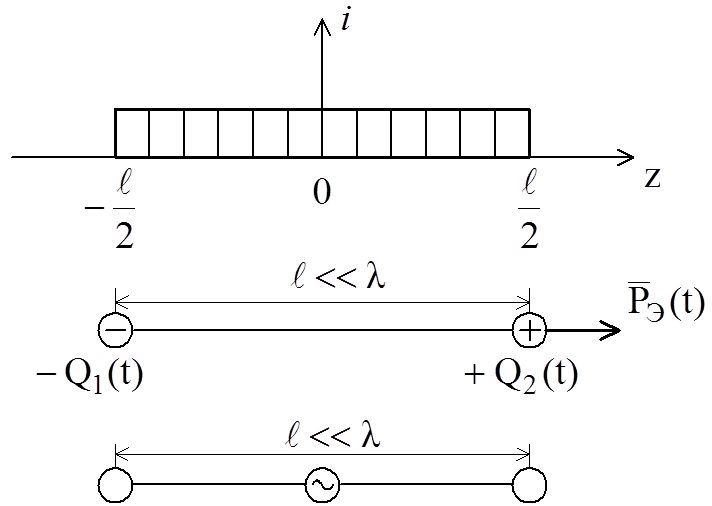 |
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.